题目内容
【题目】如图,已知平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 为边
为边![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻折成
翻折成![]() .若
.若![]() 为线段
为线段![]() 的中点,则在
的中点,则在![]() 翻折过程中,有下列三个命题:
翻折过程中,有下列三个命题:
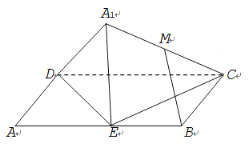
①线段![]() 的长是定值;
的长是定值;
②存在某个位置,使![]() ;
;
③存在某个位置,使![]() 平面
平面![]() .
.
其中正确的命题有______. (填写所有正确命题的编号)
【答案】①③
【解析】
取![]() 中点
中点![]() ,连接
,连接![]() ,利用中位线的性质去证明平面
,利用中位线的性质去证明平面![]() 平面
平面![]() ,即可证明
,即可证明![]() 平面
平面![]() ;由平面
;由平面![]() 平面
平面![]() 可得
可得![]() ,由余弦定理可得
,由余弦定理可得![]() ,进而求证即可;由题可证得
,进而求证即可;由题可证得![]() ,若
,若![]() 成立,则
成立,则![]() 平面
平面![]() ,与
,与![]() 是等边三角形矛盾,即可判断
是等边三角形矛盾,即可判断
取![]() 中点
中点![]() ,连接
,连接![]() ,
,

则![]() ,
,![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,故③正确;
,故③正确;
由题![]() ,则
,则![]() ,由
,由![]() ,
,![]() 定值,
定值,![]() 定值,故由余弦定理可得
定值,故由余弦定理可得![]() , 所以
, 所以![]() 是定值,故①正确;
是定值,故①正确;
由题,![]() 是等边三角形,则
是等边三角形,则![]() ,又平行四边形
,又平行四边形![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() ,即
,即![]() ,
,
若![]() ,则
,则![]() 平面
平面![]() ,所以
,所以![]() ,与
,与![]() 是等边三角形矛盾,故②错误;
是等边三角形矛盾,故②错误;
故答案为:①③

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目