Question

【题目】已知椭圆及点，若直线与椭圆交于点，且（ 为坐标原点），椭圆的离心率为.

（1）求椭圆的标准方程；

（2）若斜率为的直线交椭圆于不同的两点，求面积的最大值.

Answer 1

【答案】(1) ；(2)1.

【解析】试题分析： 由椭圆的离心率公式得到，设点在第一象限，由椭圆的对称性可知，所以，进而求得点的坐标，然后联立方程求得，即可得到椭圆的标准方程；

设直线的方程为，联立椭圆方程，求得或，设，求出的值，又由题意得， 到直线的距离，进而求得面积的最大值

解析：（1）由椭圆的离心率为，得，所以.

设点在第一象限，由椭圆的对称性可知，所以，

因为点坐标为，所以点坐标为，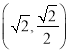

代入椭圆的方程得，与联立，

可得，所以椭圆的标准方程为.

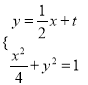（2）设直线的方程为，由得.

由题意得， ，

整理得，所以或.

设，则，

所以

.

又由题意得， 到直线的距离.

的面积

当且仅当，即时取等号，且此时满足，

所以面积的最大值为1.