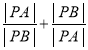题目内容
【题目】已知动圆经过定点![]() ,且与定直线
,且与定直线![]() 相切.
相切.
(1)求动圆圆心![]() 的轨迹方程
的轨迹方程![]() ;
;
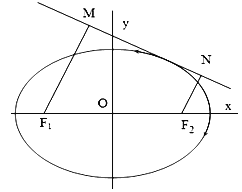
(2)已知点![]() ,过点
,过点![]() 作直线
作直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 轴的垂线分别与直线
轴的垂线分别与直线![]() ,
,![]() 交于点
交于点![]() ,
,![]() (
(![]() 为原点),求证:
为原点),求证:![]() 为线段
为线段![]() 中点.
中点.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)根据抛物线的定义,可得圆心![]() 的轨迹是以
的轨迹是以![]() 为焦点,
为焦点,![]() 为准线的抛物线,从而得出方程;
为准线的抛物线,从而得出方程;
(2)设![]() ,
,![]() ,设直线斜率为
,设直线斜率为![]() ,则直线方程为
,则直线方程为![]() ,与抛物线联立得出
,与抛物线联立得出![]() ,且
,且![]() ,写出韦达定理
,写出韦达定理![]() ,
,![]() ,再通过直线的交点分别求出
,再通过直线的交点分别求出![]() 和
和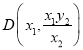 ,从而求出
,从而求出![]() ,结合韦达定理,化简得
,结合韦达定理,化简得![]() ,即可证出:
,即可证出:![]() 为线段
为线段![]() 中点.
中点.
解:(1)由题意知,动圆圆心![]() 到定点
到定点![]() 的距离与到定直线
的距离与到定直线![]() 的距离相等,
的距离相等,
由抛物线定义知,
动圆圆心![]() 的轨迹是以
的轨迹是以![]() 为焦点,
为焦点,![]() 为准线的抛物线,
为准线的抛物线,
其中![]() ,
,
即动圆圆心![]() 的轨迹方程
的轨迹方程![]() 为:
为:![]() .
.
(2)设![]() ,
,![]() ,显然直线
,显然直线![]() 斜率存在且不为0,设为
斜率存在且不为0,设为![]() ,
,
则直线方程为![]() ,
,
将![]() 与抛物线方程
与抛物线方程![]() :
:![]() 联立,
联立,
得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
又![]() ,联立
,联立![]() 得
得![]() ,
,
同理可得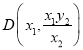 ,
,
则![]()
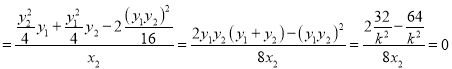 ,
,
即![]() ,
,
所以![]() 为线段
为线段![]() 中点.
中点.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】炼钢是一个氧化降碳的过程,由于钢水含碳量的多少直接影响冶炼时间的长短,因此必须掌握钢水含碳量和冶炼时间的关系.现已测得炉料熔化完毕时钢水的含碳量![]() 与冶炼时间
与冶炼时间![]() (从炉料熔化完毕到出钢的时间)的一组数据,如下表所示:
(从炉料熔化完毕到出钢的时间)的一组数据,如下表所示:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 104 | 180 | 190 | 177 | 147 | 134 | 150 | 191 | 204 | 121 |
| 100 | 200 | 210 | 185 | 155 | 135 | 170 | 205 | 235 | 125 |
| 10400 | 36000 | 39900 | 32745 | 22785 | 18090 | 25500 | 39155 | 47940 | 15125 |
(1)据统计表明,![]() 与
与![]() 之间具有线性相关关系,请用相关系数
之间具有线性相关关系,请用相关系数![]() 加以说明(
加以说明(![]()
![]() ,则认为
,则认为![]() 与
与![]() 有较强的线性相关关系,否则认为没有较强的线性相关关系,
有较强的线性相关关系,否则认为没有较强的线性相关关系,![]() 精确到0.001);
精确到0.001);
(2)建立![]() 关于
关于![]() 的回归方程(回归系数的结果精确到0.01);
的回归方程(回归系数的结果精确到0.01);
(3)根据(2)中的结论,预测钢水含碳量为160个0.01%的冶炼时间.
参考公式:回归方程![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为 ,
,
![]() ,相关系数
,相关系数
参考数据: ,
,
![]() .
.