题目内容
已知平面直角坐标系xOy中O是坐标原点,A(6,2| 3 |
| 3 |
(1)求圆C的方程及直线l的方程;
(2)设圆N的方程(x-4-7cosθ)2+(y-7sinθ)2=1,(θ∈R),过圆N上任意一点P作圆C的两条切线PE,PF,切点为E,F,求
| CE |
| CF |
分析:(1)直角三角形斜边的中点就是该直角三角形外接圆的圆心,半径r、弦长l、弦心距d三者满足:r2=d2+(
)2.
(2)结合图象,利用2个向量的数量积的定义,用∠ECF的一半α表示则
•
的结果,由圆的几何性质|PC|≥|NC|-1,可得cosα的最大值,进而得
•
的最大值.
| l |
| 2 |
(2)结合图象,利用2个向量的数量积的定义,用∠ECF的一半α表示则
| CE |
| CF |
| CE |
| CF |
解答:解:(1)因为A(6,2
),B(8,0),所以△OAB为以OB为斜边的直角三角形,
所以圆C:(x-4)2+y2=16
①斜率不存在时,l:x=2被圆截得弦长为4
,所以l:x=2适合
②斜率存在时,设l:y-6=k(x-2)即kx-y+6-2k=0
因为被圆截得弦长为4
,所以圆心到直线距离为2,所以
=2
∴k=-
∴l:y-6=-
(x-2),即4x+3y-26=0
综上,l:x=2或4x+3y-26=0
(2)解:设∠ECF=2a,
则
•
=|
|•|
|•cos2α=16cos2α=32cos2α-16.
在Rt△PCE中,cosα=
=
,由圆的几何性质得|PC|≥|NC|-1=7-1=6,
所以cosα≤
,
由此可得
•
≤-
,则
•
的最大值为-
.
| 3 |
所以圆C:(x-4)2+y2=16
①斜率不存在时,l:x=2被圆截得弦长为4
| 3 |
②斜率存在时,设l:y-6=k(x-2)即kx-y+6-2k=0
因为被圆截得弦长为4
| 3 |
| |4k+6-2k| | ||
|
∴k=-
| 4 |
| 3 |
∴l:y-6=-
| 4 |
| 3 |
综上,l:x=2或4x+3y-26=0
(2)解:设∠ECF=2a,
则
| CE |
| CF |
| CE |
| CF |
在Rt△PCE中,cosα=
| x |
| |PC| |
| 4 |
| |PC| |
所以cosα≤
| 2 |
| 3 |
由此可得
| CE |
| CF |
| 16 |
| 9 |
| CE |
| CF |
| 16 |
| 9 |
点评:本题属于应用直线和圆的位置关系,并结合平面向量数量积的预算,求最值问题.

练习册系列答案
相关题目
 已知平面直角坐标系xOy上的区域D由不等式组
已知平面直角坐标系xOy上的区域D由不等式组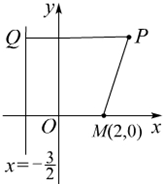 已知平面直角坐标系xOy上的定点M(2,0)和定直线l:x=
已知平面直角坐标系xOy上的定点M(2,0)和定直线l:x=