题目内容
 如图,正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为
如图,正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为| 2 |
(1)建立适当的坐标系,并写出点A,B,A1,C1的坐标;
(2)求AC1与侧面ABB1A1所成的角.
分析:(1)以点A为坐标原点O,以AB所成直线为Oy轴,以AA1所在直线为Oz轴,以经过原点且与平面ABB1A1垂直的直线为Ox轴,建立空间直角坐标系,可求出A,B,A1,C1的坐标;
(2)取A1B1的中点M,易证AC1与AM所成的角就是AC1与侧面ABB1A1所成的角,求出
与
的坐标,利用向量的夹角公式求出此角即可.
(2)取A1B1的中点M,易证AC1与AM所成的角就是AC1与侧面ABB1A1所成的角,求出
| AC1 |
| AM |
解答: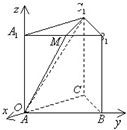 解:①如图,以点A为坐标原点O,以AB所成直线为Oy轴,
解:①如图,以点A为坐标原点O,以AB所成直线为Oy轴,
以AA1所在直线为Oz轴,以经过原点且与平面ABB1A1垂直的直线为Ox轴,建立空间直角坐标系.
由已知得A(0,0,0),B(0,a,0),A1(0,0,
a),C1(-
a,
,
a).
②坐标系如上,取A1B1的中点M,于是有M(0,
,
a),
连AM,MC1有
=(-
a,0,0),
且
=(0,a,0),
=(0,0,
a),
由
•
=0,
•
=0,
所以,MC1⊥面ABB1A1,
∴AC1与AM所成的角就是AC1与侧面ABB1A1所成的角.
∵
=(-
a,
,
a),
=(0,
,
a),
∴
•
=0+
+2a2=
a2,|
|=
=
a,|
|=
=
a,
∴cos<
,
>=
=
,
所以,
与
所成的角,即AC1与侧面ABB1A1所成的角为30°.
 解:①如图,以点A为坐标原点O,以AB所成直线为Oy轴,
解:①如图,以点A为坐标原点O,以AB所成直线为Oy轴,以AA1所在直线为Oz轴,以经过原点且与平面ABB1A1垂直的直线为Ox轴,建立空间直角坐标系.
由已知得A(0,0,0),B(0,a,0),A1(0,0,
| 2 |
| ||
| 2 |
| a |
| 2 |
| 2 |
②坐标系如上,取A1B1的中点M,于是有M(0,
| a |
| 2 |
| 2 |
连AM,MC1有
| MC1 |
| ||
| 2 |
且
| AB |
| AA1 |
| 2 |
由
| MC1 |
| AB |
| MC1 |
| AA1 |
所以,MC1⊥面ABB1A1,
∴AC1与AM所成的角就是AC1与侧面ABB1A1所成的角.
∵
| AC1 |
| ||
| 2 |
| a |
| 2 |
| 2 |
| AM |
| a |
| 2 |
| 2 |
∴
| AC1 |
| AM |
| a2 |
| 4 |
| 9 |
| 4 |
| AC1 |
|
| 3 |
| AM |
|
| 3 |
| 2 |
∴cos<
| AC1 |
| AM |
| ||||
|
| ||
| 2 |
所以,
| AC1 |
| AM |
点评:本题主要考查了直线与平面之间的位置关系,考查空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
 如图,正三棱柱ABC-A1B1C1的各棱长都2,E,F分别是AB,A1C1的中点,则EF的长是( )
如图,正三棱柱ABC-A1B1C1的各棱长都2,E,F分别是AB,A1C1的中点,则EF的长是( )| A、2 | ||
B、
| ||
C、
| ||
D、
|
 如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点.
如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点. 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点. (2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点. 如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.
如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.