题目内容
3.抛物线x2=2py(p>0)的焦点为F,其准线与双曲线$\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{3}$=1相交于A,B两点,若△ABF为等边三角形,则△ABF的面积为12$\sqrt{3}$.分析 求出抛物线的焦点坐标,准线方程,然后求出抛物线的准线与双曲线的交点坐标,利用三角形是等边三角形求出p,即可求出△ABF的面积.
解答 解:抛物线的焦点坐标为(0,$\frac{p}{2}$),准线方程为:y=-$\frac{p}{2}$,
准线方程与双曲线联立可得:$\frac{{x}^{2}}{3}-\frac{(-\frac{p}{2})^{2}}{3}$=1,
解得x=±$\sqrt{3+\frac{{p}^{2}}{4}}$,
因为△ABF为等边三角形,所以$\sqrt{{p}^{2}+{x}^{2}}=2|x|$,即p2=3x2,
即${p}^{2}=3(3+\frac{{p}^{2}}{4})$,解得p=6.
所以x2=12,
所以△ABF的面积为$\frac{\sqrt{3}}{4}•4{x}^{2}$=12$\sqrt{3}$.
故答案为:12$\sqrt{3}$.
点评 本题考查抛物线的简单性质,双曲线方程的应用,考查分析问题解决问题的能力以及计算能力.

练习册系列答案
相关题目
8.已知{an}是等差数列,a1+a2=4,a7+a8=28,则公差等于( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
13.下列函数中最小正周期为π且为偶函数的是( )
| A. | y=|sinx| | B. | y=tan$\frac{x}{2}$ | C. | y=-sin2x | D. | y=cos4x |
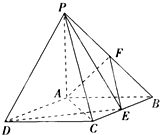 如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在棱BC上移动.
如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在棱BC上移动.