题目内容
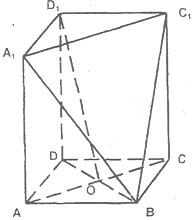
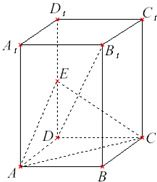
如图在平行六面体ABCD-A1B1C1D1中,E、F、G分别是A1D1、D1D、D1C1的中点.
求证:平面EFG∥平面AB1C.
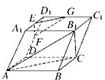
求证:平面EFG∥平面AB1C.

证明:设
=a,
=b,
=c,则
=
+
=
(a+b),
=a+b=2
,
∴
∥
,
=
+
=
b-
c=
(b-c),
=
+
=b-c=2
,
∴
∥
.
又∵EG与EF相交,AC与B1C相交,
∴平面EFG∥平面AB1C.
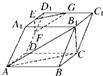
| AB |
| AD |
| AA1 |
| EG |
| ED1 |
| D1G |
| 1 |
| 2 |
| AC |
| EG |
∴
| EG |
| AC |
| EF |
| ED1 |
| D1F |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| B1C |
| B1C1 |
| C1C |
| EF |
∴
| EF |
| B1C |
又∵EG与EF相交,AC与B1C相交,
∴平面EFG∥平面AB1C.


练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目