题目内容
(本题满分12分)已知等差数列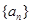 中,
中,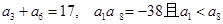 .
.
(Ⅰ)求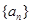 的通项公式;
的通项公式;
(Ⅱ)调整数列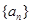 的前三项
的前三项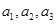 的顺序,使它成为等比数列
的顺序,使它成为等比数列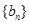 的前三项,求
的前三项,求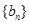 的前
的前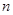 项和.
项和.
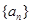 中,
中,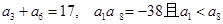 .
.(Ⅰ)求
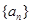 的通项公式;
的通项公式;(Ⅱ)调整数列
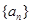 的前三项
的前三项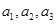 的顺序,使它成为等比数列
的顺序,使它成为等比数列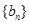 的前三项,求
的前三项,求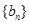 的前
的前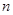 项和.
项和.(Ⅰ)an=3n-5.
(Ⅱ)(i) .
.
(ii) 。
。
(Ⅱ)(i)
 .
.(ii)
 。
。试题分析:(1)先利用已知条件求得a1=-2,a8=19进而求出公差即可求{an}的通项公式;
(2)先求出数列{an}的前三项再利用等比数列满足的条件进行调整,求出等比数列{bn}的前三项,知道首项和公比,再代入等比数列的求和公式即可求出{bn}的前n项和.
解:(Ⅰ)由已知,得
 ----- -----------1分
----- -----------1分又
 ,∴
,∴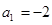 ,
, ,∴
,∴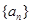 的公差d=3 -----3分
的公差d=3 -----3分∴an=a1+(n-1)d=-2+3(n-1)=3n-5. ---------------------------6分
(Ⅱ)由(Ⅰ),得a1=-2,a2=1,a3=4.
依题意可得:数列{bn}的前三项为b1=1,b2=-2,b3=4或b1==4,b2=-2,b3="1" --8分
(i)当等比数列{bn}的前三项为b1=1,b2=-2,b3=4时,则q=-2 .
 . -------------------------9分
. -------------------------9分(ii)当第比数列{bn}的前三项为b1=4,b2=-2,b3=1时,则
 .
. -------------------12分考点:
-------------------12分考点:点评:解决该试题的关键是在对等比数列进行求和时,一定要先看等比数列的公比是否为1,再代入求和公式。

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
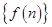 的前n项和为
的前n项和为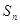 ,且
,且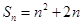 .
.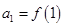 ,
,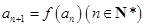 ,求证数列
,求证数列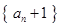 是等比数列,并求数
是等比数列,并求数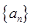 的前
的前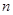 项和
项和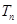 .
. 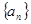 满足
满足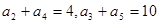 ,则前10项和
,则前10项和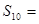
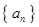 是各项均不为0的等差数列,公差为d,
是各项均不为0的等差数列,公差为d,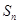 为其前n项和,且满足
为其前n项和,且满足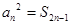 ,
,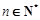 .数列
.数列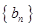 满足
满足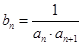 ,
,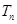 为数列
为数列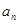 和数列
和数列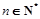 ,不等式
,不等式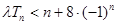 恒成立,求实数
恒成立,求实数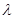 的取值范围;
的取值范围;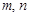
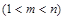 ,使得
,使得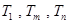 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有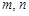 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.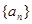 为等差数列,公差
为等差数列,公差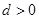 ,
,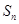 是数列
是数列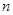 项和, 且
项和, 且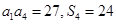 .
.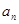 ;(2)令
;(2)令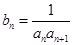 ,求数列
,求数列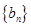 的前
的前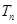 .
.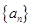 的前
的前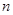 项和为
项和为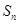
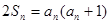
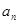
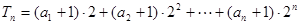 ,求
,求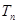
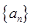 满足:
满足: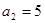 ,
,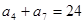 ,
,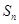 .
.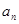 及前n项和
及前n项和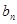 =
=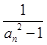 (n
(n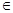 N*),求数列
N*),求数列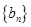 的前n项和
的前n项和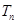 .
.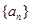 中,
中, 且
且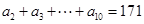 ,则公差
,则公差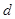 =
=