题目内容
【题目】已知顶点在原点,焦点在x轴的负半轴的抛物线截直线y=x+![]() 所得的弦长|P1P2|=4
所得的弦长|P1P2|=4![]() ,求此抛物线的方程.
,求此抛物线的方程.
【答案】y2=-2x.
【解析】试题分析:抛物线![]() ,联立
,联立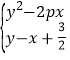 ,得
,得![]() ,由
,由![]() ,根据韦达定理及弦长公式,列出关于
,根据韦达定理及弦长公式,列出关于![]() 的方程,解得
的方程,解得![]() 的值,就能求出抛物线方程.
的值,就能求出抛物线方程.
试题解析:设抛物线方程为y2=-2px(p>0),把直线方程与抛物线方程联立得
消元得x2+(3+2p)x+![]() =0,① 判别式Δ=(3+2p)2-9=4p2+12p>0,解得p>0或p<-3(舍),
=0,① 判别式Δ=(3+2p)2-9=4p2+12p>0,解得p>0或p<-3(舍),
设P1(x1,y1),P2(x2,y2),则①中由根与系数的关系得x1+x2=-(3+2p),x1·x2=![]() ,代入弦长公式得
,代入弦长公式得![]() ·
·![]() =4
=4![]() ,解得p=1或p=-4(舍),所以所求抛物线方程为y2=-2x.
,解得p=1或p=-4(舍),所以所求抛物线方程为y2=-2x.

练习册系列答案
相关题目



