题目内容
13. 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.(Ⅰ)求证:BM∥平面ADEF;
(Ⅱ) 求证:平面EDB⊥平面BCE
(Ⅲ)求三棱锥M-BDE的体积.
分析 (I)取DE中点N,连接MN,AN,由三角形中位线定理,结合已知中AB∥CD,AB=AD=2,CD=4,易得四边形ABMN为平行四边形,所以BM∥AN,再由线面平面的判定定理,可得BM∥平面ADEF;
(II)由已知中正方形ADEF与梯形ABCD所在的平面互相垂直,易得ED⊥平面ABCD,进而ED⊥BC,由勾股定理,我们易判断出△BCD中,BC⊥BD,由线面垂直的判定定理可得BC⊥平面BDE,再由面面垂直的判定定理,即可得到平面BDE⊥平面BEC;
(III)利用三棱锥的体积计算公式可得VM-BDE=VB-DEM.
解答 (I)证明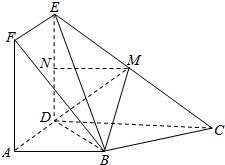 :取DE中点N,连接MN,AN
:取DE中点N,连接MN,AN
在△EDC中,M、N分别为EC,ED的中点,所以MN∥CD,且MN=$\frac{1}{2}$CD.
由已知AB∥CD,AB=$\frac{1}{2}$CD,所以MN∥AB,且MN=AB.
所以四边形ABMN为平行四边形,所以BM∥AN
又因为AN?平面ADEF,
且BM?平面ADEF,
所以BM∥平面ADEF.
(II)证明:在正方形ADEF中,ED⊥AD,
又因为平面ADEF⊥平面ABCD,
且平面ADEF∩平面ABCD=AD,
所以ED⊥平面ABCD,所以ED⊥BC.
在直角梯形ABCD中,
AB=AD=2,CD=4,可得BC=2$\sqrt{2}$
在△BCD中,BD=BC=2$\sqrt{2}$,CD=4,
所以BC⊥BD.
所以BC⊥平面BDE,又因为BC?平面BCE,
所以平面BDE⊥平面BEC.
(III)解:因为M为EC的中点,
所以${S}_{△DEM}=\frac{1}{2}{S}_{△CDE}=2$,
因为AD⊥CD,AD⊥DE,且DE与CD相交于D
所以AD⊥平面CDE.
因为AB∥CD,
所以三棱锥B-DME的高=AD=2,
所以VM-BDE=VB-DEM=$\frac{1}{3}{S}_{△DEM}•AD=\frac{4}{3}$.
点评 本题考查的知识点是二面角的平面角及求法,直线与平面平行的判定,平面与平面垂直的判定,熟练掌握空间直线与平面不同位置关系(平行和垂直)的判定定理、性质定理、定义及几何特征是解答本题的关键.


| A. | 相交 | B. | 平行 | C. | 异面而且垂直 | D. | 异面但不垂直 |
| A. | 2条 | B. | 4条 | C. | 6条 | D. | 8条 |
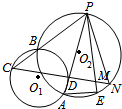 如图,已知⊙O1与⊙O2相交于A、B两点,P是⊙O1上一点,PB的延长线交⊙O2于点C,PA交⊙O2于点D,CD的延长线交⊙O1于点N.
如图,已知⊙O1与⊙O2相交于A、B两点,P是⊙O1上一点,PB的延长线交⊙O2于点C,PA交⊙O2于点D,CD的延长线交⊙O1于点N. 一般齿轮传动装置中有一个主动轮O2和一个从动轮O1,用皮带连接(假设皮带与轮子之间不发生滑动),直线O1O2是一条水平直线,主动轮O2的半径是R,从动轮O1的半径是r,且R=2r,主动轮每分钟逆时针转30圈.开始转动时,从动轮、主动轮上分别标有A1,A2两个点(如图所示),经过t秒A1,A2两个点运动到新位置B1,B2,设B1,B2到水平线O1O2的垂直高度(当A1,A2运动到水平线O1O2下方时,高度是负值)分别是h1,h2.
一般齿轮传动装置中有一个主动轮O2和一个从动轮O1,用皮带连接(假设皮带与轮子之间不发生滑动),直线O1O2是一条水平直线,主动轮O2的半径是R,从动轮O1的半径是r,且R=2r,主动轮每分钟逆时针转30圈.开始转动时,从动轮、主动轮上分别标有A1,A2两个点(如图所示),经过t秒A1,A2两个点运动到新位置B1,B2,设B1,B2到水平线O1O2的垂直高度(当A1,A2运动到水平线O1O2下方时,高度是负值)分别是h1,h2. 长方体ABCD-A1B1C1D1中,AA1=$\sqrt{2}$,AB=BC=2,O是底面对角线的交点.
长方体ABCD-A1B1C1D1中,AA1=$\sqrt{2}$,AB=BC=2,O是底面对角线的交点.