题目内容
(本小题满分12分)已知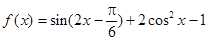
(Ⅰ)求函数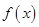 的单调增区间
的单调增区间
(Ⅱ)在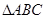 中,
中,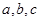 分别是角
分别是角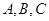 的对边,且
的对边,且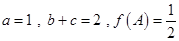 ,求
,求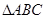 的面积.
的面积.
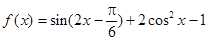
(Ⅰ)求函数
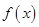 的单调增区间
的单调增区间(Ⅱ)在
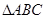 中,
中,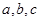 分别是角
分别是角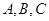 的对边,且
的对边,且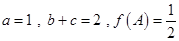 ,求
,求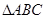 的面积.
的面积.(Ⅰ)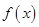 的单调递增区间是[
的单调递增区间是[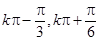 ](
](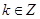 );
);
(Ⅱ) S△ABC=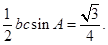
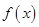 的单调递增区间是[
的单调递增区间是[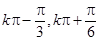 ](
](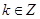 );
);(Ⅱ) S△ABC=
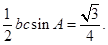
(I)先借助三角恒等变换公式把f(x)进行化简为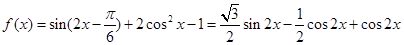
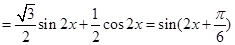 ,然后再利用正弦函数的单调增区间来求出f(x)的单调增区间.
,然后再利用正弦函数的单调增区间来求出f(x)的单调增区间.
(II)在(I)的基础上,利用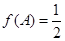 ,可求出A角,再利用
,可求出A角,再利用
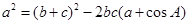 求出
求出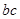 ,从而利用公式
,从而利用公式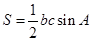 求出面积.
求出面积.
(Ⅰ)因为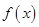 =
=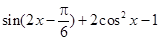 =
=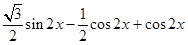
=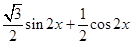 =
=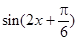 …………(3分)
…………(3分)
所以函数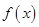 的单调递增区间是[
的单调递增区间是[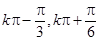 ](
](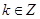 )……………(5分)
)……………(5分)
(Ⅱ)因为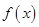 =
=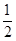 ,所以
,所以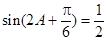 ,又
,又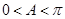 ,所以
,所以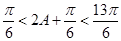 ,从而
,从而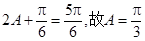 …………(7分)
…………(7分)
在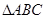 中,∵
中,∵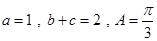 ∴1=b2+c2-2bccosA,即1=4-3bc.故bc=1(10分)
∴1=b2+c2-2bccosA,即1=4-3bc.故bc=1(10分)
从而S△ABC=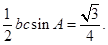 …………(12分)
…………(12分)
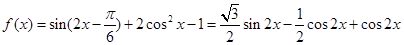
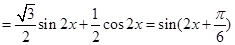 ,然后再利用正弦函数的单调增区间来求出f(x)的单调增区间.
,然后再利用正弦函数的单调增区间来求出f(x)的单调增区间.(II)在(I)的基础上,利用
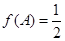 ,可求出A角,再利用
,可求出A角,再利用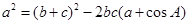 求出
求出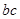 ,从而利用公式
,从而利用公式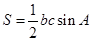 求出面积.
求出面积.(Ⅰ)因为
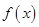 =
=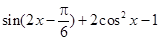 =
=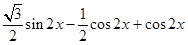
=
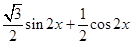 =
=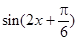 …………(3分)
…………(3分)所以函数
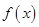 的单调递增区间是[
的单调递增区间是[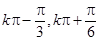 ](
](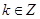 )……………(5分)
)……………(5分)(Ⅱ)因为
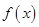 =
=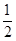 ,所以
,所以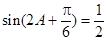 ,又
,又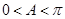 ,所以
,所以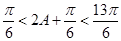 ,从而
,从而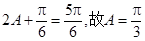 …………(7分)
…………(7分)在
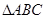 中,∵
中,∵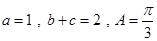 ∴1=b2+c2-2bccosA,即1=4-3bc.故bc=1(10分)
∴1=b2+c2-2bccosA,即1=4-3bc.故bc=1(10分)从而S△ABC=
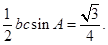 …………(12分)
…………(12分)
练习册系列答案
相关题目
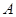 ,
,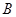 ,
,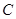 的对边分别为
的对边分别为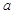 ,
,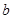 ,
,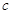 ,其中
,其中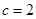 , 且
, 且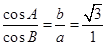
 是直角三角形;
是直角三角形;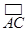 上,
上,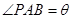 ,用
,用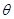 的三角函数表示三角形
的三角函数表示三角形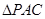 的面积,并求
的面积,并求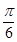 )(其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为
)(其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为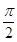 ,且图象上一个最低点为M(
,且图象上一个最低点为M(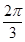 ,-2).
,-2).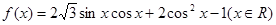 。
。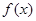 的最小正周期及在区间
的最小正周期及在区间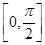 上的最大值和最小值;
上的最大值和最小值;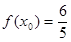 ,
,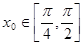 ,求
,求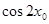 的值。
的值。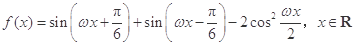 (其中
(其中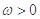 ).
).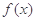 的值域;
的值域; 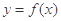 的图象与直线
的图象与直线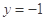 的两个相邻交点间的距离为
的两个相邻交点间的距离为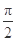 ,求函数
,求函数 x在[-
x在[-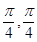 ]上单调递增,则正实数
]上单调递增,则正实数 的图象,只需将函数
的图象,只需将函数 的图象( )
的图象( ) 向右平移
向右平移 个单位
个单位  向左平移
向左平移 向右平移
向右平移 个单位
个单位  向左平移
向左平移 运算:
运算: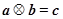 ,若
,若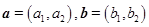 ,则向量
,则向量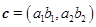 .已知
.已知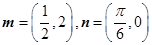 ,且点
,且点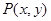 在函数
在函数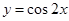 的图象上运动,点
的图象上运动,点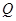 在函数
在函数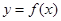 的图象上运动,且点
的图象上运动,且点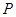 和点
和点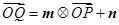 (其中
(其中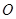 为坐标原点),则函数
为坐标原点),则函数 及最小正周期
及最小正周期 分别为( )
分别为( ) 



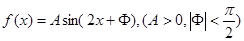 的部分图象过点(0,2),如图所示,则函数
的部分图象过点(0,2),如图所示,则函数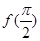 的值为 .
的值为 .