Question

【题目】已知数列是等差数列，数列是等比数列，且，的前n项和为.若对任意的恒成立.

（1）求数列，的通项公式；

（2）若数列满足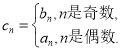问：是否存在正整数，使得，若存在求出的值，若不存在，说明理由；

（3）若存在各项均为正整数公差为的无穷等差数列，满足，且存在正整数，使得成等比数列，求的所有可能的值.

Answer 1

【答案】（1），.（2）存在，的值为5和 .（3）或.

【解析】

（1）由题意可知，从而有，做差得到，代入基本量计算可求出数列，的通项公式. （2）讨论为奇数和偶数两种情况，分别代入求解计算. （3）设的公差为，则且，若，则肯定成立，只需讨论时的情况即可.

（1）当时，，由，得；

由得①，当时有： ②，

由②-①得.

分别令可得：，.设的公差为，的公比为，

则 解得或

经检验符合条件，不合题意，舍去.

故，.

（2）

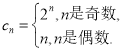
当是奇数时，由，可得，即，

所以，解得，

考虑到在正整数集上分别单调递增和递减，

故不存在其他解，即是惟一解.

当是偶数时，由可得：，

即，是偶数符合条件.

综上的值为5和.

（3）由（1），设的公差为，则且，

当时，显然成立；

当时，

所以，，

由，得，

即，

所以，

因为，所以，

即，

所以

故，

由，得，

从而要使，只要，

又，

综上，.