题目内容
已知
(Ⅰ)若 ,求
,求 的表达式;
的表达式;
(Ⅱ)若函数 和函数
和函数 的图象关于原点对称,求函数
的图象关于原点对称,求函数 的解析式;
的解析式;
(Ⅲ)若 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.
(1)f(x)=sin2x+2sinx
(2)g(x)= -sin2x+2sinx
(3)  .
.
解析试题分析:(1)
=2+sinx-C.os2x-1+sinx=sin2x+2sinx
(2)设函数y="f" (x)的图象上任一点M(x0,y0)关于原点的对称点为N(x,y)
则x0= -x,y0= -y
∵点M在函数y="f" (x)的图象上 ,即y= -sin2x+2sinx
,即y= -sin2x+2sinx
∴函数g(x)的解析式为g(x)= -sin2x+2sinx
(3) 设sinx=t,(-1≤t≤1)
设sinx=t,(-1≤t≤1)
则有
①当 时,h(t)=4t+1在[-1,1]上是增函数,∴λ= -1
时,h(t)=4t+1在[-1,1]上是增函数,∴λ= -1
②当 时,对称轴方程为直线
时,对称轴方程为直线 .
.
ⅰ)  时,
时, ,解得
,解得
ⅱ)当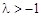 时,
时, ,解得
,解得
综上, .
.
考点:本题主要考查向量的坐标运算,三角函数的性质,三角函数恒等变换,二次函数图象和性质。
点评:典型题,本题较好地把向量、三角函数、二次函数结合在一起进行考查,体现了高考考查的重点,本题运用了换元思想,也很好地运用了转化与化归思想。

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 ,
,
 时,求
时,求 的最大值和最小值
的最大值和最小值
 ,求
,求 的取值范围
的取值范围
 .
. 的最小正周期;
的最小正周期; 时,求函数
时,求函数

 ,
, 的最小值是
的最小值是 ,最大值是
,最大值是 ,求实数
,求实数 的值.
的值. 的图象的一部分如下图所示。
的图象的一部分如下图所示。
 的解析式;
的解析式;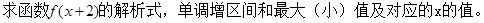
 .
. 的最大值及最小正周期;
的最大值及最小正周期; 满足
满足 ,求
,求 求下列各式的值:
求下列各式的值: ; (2)
; (2) ; (3)
; (3)
 .
. 的最小正周期和单调递减区间;
的最小正周期和单调递减区间; ,求
,求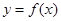 为减函数,
为减函数, 对
对 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.