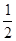题目内容
已知数列 ,
,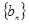 满足:
满足: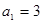 ,当
,当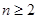 时,
时,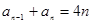 ;对于任意的正整数
;对于任意的正整数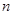 ,
,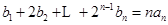 .设
.设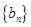 的前
的前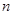 项和为
项和为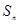 .
.
(1)计算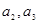 ,并求数列
,并求数列 的通项公式;
的通项公式;
(2)求满足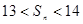 的
的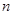 的集合.
的集合.
 ,
,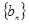 满足:
满足: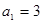 ,当
,当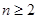 时,
时,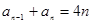 ;对于任意的正整数
;对于任意的正整数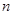 ,
,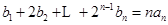 .设
.设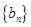 的前
的前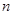 项和为
项和为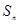 .
.(1)计算
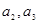 ,并求数列
,并求数列 的通项公式;
的通项公式;
(2)求满足
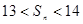 的
的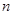 的集合.
的集合.(1)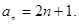 (2)
(2)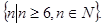
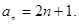 (2)
(2)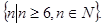
(1)先求出数列 的通项公式是求解本题的关键.由
的通项公式是求解本题的关键.由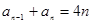 及
及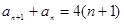 两式相减可得:
两式相减可得: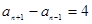 ,所以数列
,所以数列 的奇数项和偶数项各自成等差数列,公差为
的奇数项和偶数项各自成等差数列,公差为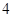 ,而
,而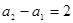 ,故
,故 是公差为
是公差为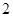 的等差数列.
的等差数列.
(2)在第(1)问的基础上,可求出{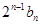 }的通项公式,进而求出
}的通项公式,进而求出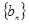 的通项公式.
的通项公式.
然后再根据通项公式的特点采用数列求和的方法求和,之后再确定sn的单调性进而确定其取值范围.
解:(1)在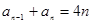 中,取
中,取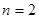 ,得
,得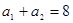 ,又,
,又,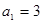 ,故
,故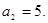 同样取
同样取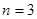 可得
可得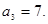 ……………………
……………………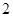 分
分
由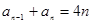 及
及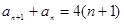 两式相减可得:
两式相减可得: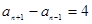 ,所以数列
,所以数列 的奇数项和偶数项各自成等差数列,公差为
的奇数项和偶数项各自成等差数列,公差为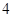 ,而
,而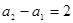 ,故
,故 是公差为
是公差为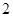 的等差数列,
的等差数列,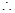
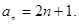 ……………………
……………………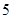 分
分
注:猜想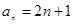 而未能证明的扣
而未能证明的扣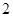 分;用数学归纳法证明不扣分.
分;用数学归纳法证明不扣分.
(2)在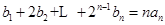 中令
中令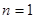 得
得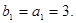 ……………………
……………………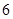 分
分
又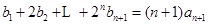 ,与
,与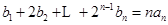 两式相减可得:
两式相减可得: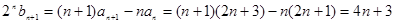 ,
, ,即当
,即当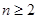 时,
时,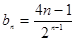
经检验,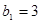 也符合该式,所以,
也符合该式,所以,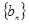 的通项公式为
的通项公式为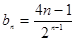 ………………9分
………………9分
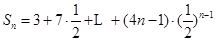 .
.
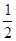
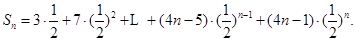
相减可得: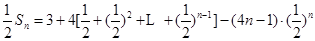
利用等比数列求和公式并化简得: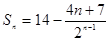 ……………………11分
……………………11分
可见,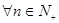 ,
, ……………………12分
……………………12分
经计算, ,注意到
,注意到 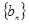 的各项为正,故
的各项为正,故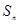 单调递增,所以满足
单调递增,所以满足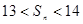 的
的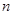 的集合为
的集合为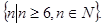 ……………………14分.
……………………14分.
 的通项公式是求解本题的关键.由
的通项公式是求解本题的关键.由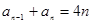 及
及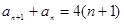 两式相减可得:
两式相减可得: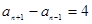 ,所以数列
,所以数列 的奇数项和偶数项各自成等差数列,公差为
的奇数项和偶数项各自成等差数列,公差为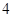 ,而
,而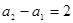 ,故
,故 是公差为
是公差为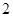 的等差数列.
的等差数列.(2)在第(1)问的基础上,可求出{
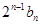 }的通项公式,进而求出
}的通项公式,进而求出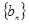 的通项公式.
的通项公式.然后再根据通项公式的特点采用数列求和的方法求和,之后再确定sn的单调性进而确定其取值范围.
解:(1)在
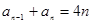 中,取
中,取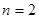 ,得
,得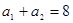 ,又,
,又,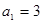 ,故
,故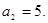 同样取
同样取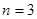 可得
可得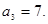 ……………………
……………………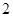 分
分由
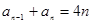 及
及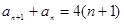 两式相减可得:
两式相减可得: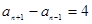 ,所以数列
,所以数列 的奇数项和偶数项各自成等差数列,公差为
的奇数项和偶数项各自成等差数列,公差为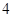 ,而
,而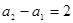 ,故
,故 是公差为
是公差为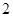 的等差数列,
的等差数列,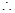
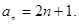 ……………………
……………………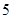 分
分注:猜想
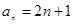 而未能证明的扣
而未能证明的扣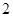 分;用数学归纳法证明不扣分.
分;用数学归纳法证明不扣分.(2)在
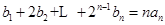 中令
中令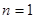 得
得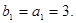 ……………………
……………………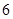 分
分又
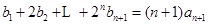 ,与
,与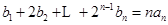 两式相减可得:
两式相减可得: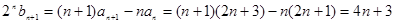 ,
, ,即当
,即当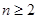 时,
时,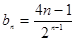
经检验,
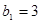 也符合该式,所以,
也符合该式,所以,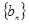 的通项公式为
的通项公式为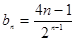 ………………9分
………………9分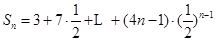 .
.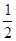
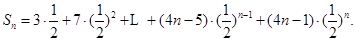
相减可得:
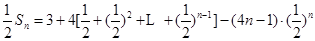
利用等比数列求和公式并化简得:
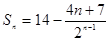 ……………………11分
……………………11分可见,
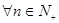 ,
, ……………………12分
……………………12分经计算,
 ,注意到
,注意到 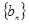 的各项为正,故
的各项为正,故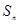 单调递增,所以满足
单调递增,所以满足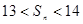 的
的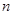 的集合为
的集合为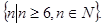 ……………………14分.
……………………14分.
练习册系列答案
相关题目
 的公比
的公比 ,前
,前 项和为
项和为 ,若
,若 ,则
,则 ( )
( )



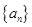 为等差数列,
为等差数列,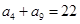 ,
,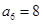 ,则
,则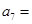 ___________.
___________.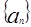 满足
满足 ,则称数列
,则称数列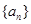 中,
中,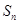 为
为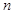 项和,
项和,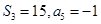 .
.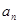 与
与 的首项
的首项 ,前
,前 项和
项和 .(Ⅰ)求数列
.(Ⅰ)求数列 ,
, ,
, 为数列
为数列 的前
的前 .
.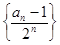 为等差数列;
为等差数列;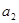 与
与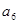 的等差中项为5,
的等差中项为5,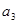 与
与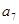 的等差中项为7,则
的等差中项为7,则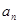 = 。
= 。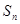 为等差数列
为等差数列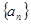 的前
的前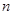 项之和,若
项之和,若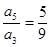 ,则
,则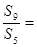 ()
()