题目内容
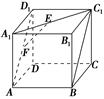
(本小题满分12分) 如图,在四棱锥 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱 ⊥底面
⊥底面 ,
, ,
, 是
是 的中点,作
的中点,作 交
交 于点
于点
(1) 证明 //平面
//平面 ;
;
(2) 证明 ⊥平面
⊥平面 ;
;
(3) 求二面角 —
— —
— 的大小。
的大小。
 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱 ⊥底面
⊥底面 ,
, ,
, 是
是 的中点,作
的中点,作 交
交 于点
于点
(1) 证明
 //平面
//平面 ;
;(2) 证明
 ⊥平面
⊥平面 ;
;(3) 求二面角
 —
— —
— 的大小。
的大小。
(1)证明:见解析;(2)证明:见解析;(3)二面角 —
— —
— 的大小为
的大小为
 —
— —
— 的大小为
的大小为
试题分析:(1)连结
 ,
, 交
交 于O,连结
于O,连结
∵底面
 是正方形,∴点O是
是正方形,∴点O是 的中点
的中点在
 中,
中, 是中位线,∴
是中位线,∴ //
//  , 得到证明。
, 得到证明。(2)∵
 ⊥底面
⊥底面 且
且 底面
底面 ,
,∴
 ∵
∵ ,可知
,可知 是等腰直角三角形,而
是等腰直角三角形,而 是斜边
是斜边 的中线,
的中线,∴
 推理得到
推理得到 平面
平面
又
 且
且 ,所以
,所以 ⊥平面
⊥平面 (3)由(2)知,
(3)由(2)知, ,
,故
 是二面角
是二面角 —
— —
— 的平面角
的平面角 解:(1)证明:连结
 ,
, 交
交 于O,连结
于O,连结
∵底面
 是正方形,∴点O是
是正方形,∴点O是 的中点
的中点在
 中,
中, 是中位线,∴
是中位线,∴ //
//  …(1分)
…(1分)而
 平面EDB且
平面EDB且 平面
平面 ,
,所以,
 // 平面
// 平面 …(3分)
…(3分)(2)证明:∵
 ⊥底面
⊥底面 且
且 底面
底面 ,
,∴

∵
 ,可知
,可知 是等腰直角三角形,而
是等腰直角三角形,而 是斜边
是斜边 的中线,
的中线,∴
 ① …(4分)
① …(4分)同样由
 ⊥底面
⊥底面 ,得
,得 ⊥
⊥
∵底面
 是正方形,有DC⊥
是正方形,有DC⊥ ,∴
,∴ ⊥平面
⊥平面 …(5分)
…(5分)而
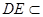 平面
平面 ,∴
,∴ ②
②由①和②推得
 平面
平面
而
 平面
平面 ,∴
,∴ …(7分)
…(7分)又
 且
且 ,所以
,所以 ⊥平面
⊥平面 …(8分)
…(8分)(3)解:由(2)知,
 ,
,故
 是二面角
是二面角 —
— —
— 的平面角 …(9分)
的平面角 …(9分)由(2)知,

设正方形ABCD的边长为
 则
则
 ,
,  ,
,
在
 中,
中,
在
 中,
中, , …(11分)
, …(11分)∴
 所以,二面角
所以,二面角 —
— —
— 的大小为
的大小为 …(12分)
…(12分)(说明:也可用向量法)
点评:解决该试题的关键是利用线面平行的判定定理和线面垂直的判定定理来得到证明,以及三垂线定理求解二面角的平面角。

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目

 上找一点M,在AD上找点N,使平面MED//平面BFN,说明理由;并求出
上找一点M,在AD上找点N,使平面MED//平面BFN,说明理由;并求出 的值
的值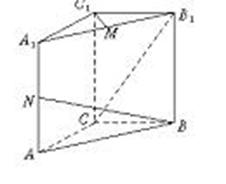
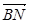 的长; (2)求cos<
的长; (2)求cos<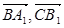 >的值; (3)求证:A1B⊥C1M.
>的值; (3)求证:A1B⊥C1M. 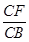 =
=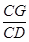 =
=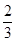 ,则( )
,则( )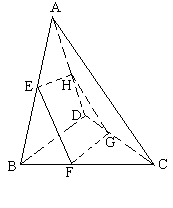
 是三个互不重合的平面,
是三个互不重合的平面, 是一条直线,则下列命题中正确的是( )
是一条直线,则下列命题中正确的是( )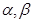 的所成角相等,则
的所成角相等,则
 ,则
,则
 的距离相等,则
的距离相等,则
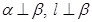 ,则
,则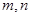 是不同的直线,
是不同的直线, 是不同的平面,给出下列命题真命题是
是不同的平面,给出下列命题真命题是  、
、 是两条不同的直线,
是两条不同的直线, 、
、 是两个不同的平面.考查下列命题,其中正确的命题是( )
是两个不同的平面.考查下列命题,其中正确的命题是( )


