题目内容
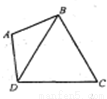
如图，已知平面四边形ABCD在平面α内的正投影是一个平行四边形AB1C1D1，求证四边形ABCD是平行四边形．
答案：
解析：
提示：
解析：
|
证明：由正投影定义知AA1∥BB1∥CC1∥DD1． 又A1B1C1D1为平行四边形，∴A1B1∥D1C1． 又AA1∩A1B1＝A1，DD1∩D1C1＝D1， ∴平面ABB1A1∥平面 DCC1D1． 又平面ABCD∩平面AB1B1A1＝AB， 平面ABCD∩平面DCC1D1＝DC， ∴AB∥DC． 同理可证，AD∥BC． ∴四边形ABCD为平行四边形． |
提示：
|
分析：利用正投影的定义及性质找出有关平行线． 解题心得：本题证明过程体现了线线平行、线面平行、面面平行相互转化的过程． |
练习册系列答案
相关题目
如图，已知平面四边形ABCD中，△BCD为正三角形，AB=AD=2，∠BAD=2θ，记四边形ABCD的面积为S．
,求P到直线BC的距离;
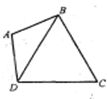如图，已知平面四边形ABCD中，△BCD为正三角形，AB=AD=2，∠BAD=2θ，记四边形ABCD的面积为S．
