题目内容
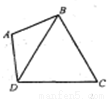
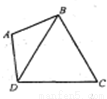
如图,已知平面四边形ABCD中,△BCD为正三角形,AB=AD=2,∠BAD=2θ,记四边形ABCD的面积为S.(1)将S表示为θ的函数;
(2)求S的最大值及相应的θ值.
【答案】分析:(1)根据题设条件合理建立方程,从而得出S关于θ的函数关系式.
(2)利用正弦函数取得最大值的结论,可以得到S的最大值及相应的θ值.
解答:解:(1)∵∠BAD=2θ,
∴△DAD中,BD2=AB2+AD2-2AB•ADcos2θ=8-8cos2θ,
∵△BCD为正三角形
∴S△BCD=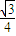 BD2=
BD2=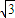 (2-2cos2θ)
(2-2cos2θ)
∴四边形ABCD的面积为S=S△BAD+S△BCD= •AB•ADsin2θ+
•AB•ADsin2θ+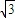 (2-2cos2θ)
(2-2cos2θ)
=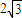 +2sin2θ-2
+2sin2θ-2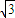 cos2θ=
cos2θ=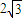 +4sin(2θ-
+4sin(2θ-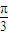 ),其中θ∈(0,
),其中θ∈(0,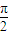 )
)
(2)由(1)得,当2θ-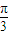 =
=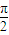 时,
时,
即θ=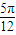 时,S的最大值为4+
时,S的最大值为4+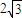 .
.
点评:本题主要考查了在实际问题中建立三角函数模型的问题.考查了学生知识的掌握和迁移的能力.挖掘题设条件,合理运用三角函数是正确解题的关键.
(2)利用正弦函数取得最大值的结论,可以得到S的最大值及相应的θ值.
解答:解:(1)∵∠BAD=2θ,
∴△DAD中,BD2=AB2+AD2-2AB•ADcos2θ=8-8cos2θ,
∵△BCD为正三角形
∴S△BCD=
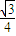 BD2=
BD2=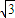 (2-2cos2θ)
(2-2cos2θ)∴四边形ABCD的面积为S=S△BAD+S△BCD=
 •AB•ADsin2θ+
•AB•ADsin2θ+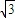 (2-2cos2θ)
(2-2cos2θ)=
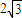 +2sin2θ-2
+2sin2θ-2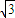 cos2θ=
cos2θ=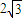 +4sin(2θ-
+4sin(2θ-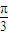 ),其中θ∈(0,
),其中θ∈(0,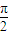 )
)(2)由(1)得,当2θ-
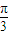 =
=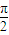 时,
时,即θ=
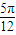 时,S的最大值为4+
时,S的最大值为4+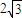 .
.点评:本题主要考查了在实际问题中建立三角函数模型的问题.考查了学生知识的掌握和迁移的能力.挖掘题设条件,合理运用三角函数是正确解题的关键.

练习册系列答案
相关题目
 如图,已知平面四边形ABCD中,△BCD为正三角形,AB=AD=2,∠BAD=2θ,记四边形ABCD的面积为S.
如图,已知平面四边形ABCD中,△BCD为正三角形,AB=AD=2,∠BAD=2θ,记四边形ABCD的面积为S.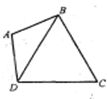 如图,已知平面四边形ABCD中,△BCD为正三角形,AB=AD=2,∠BAD=2θ,记四边形ABCD的面积为S.
如图,已知平面四边形ABCD中,△BCD为正三角形,AB=AD=2,∠BAD=2θ,记四边形ABCD的面积为S.