题目内容
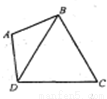
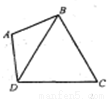
如图:已知平面四边形ABCD,AC、BD相交于O,AB=AD,CB=CD,
∠ABC=120°,且PA⊥平面ABCD.
(1)若AB=PA=![]() ,求P到直线BC的距离;
,求P到直线BC的距离;
(2)求证平面PBD⊥平面PAC.
(1)![]() (2)见解析
(2)见解析
解析:
(1)延长CB,过A在平面![]() 内作AE⊥CB,垂足为E.
内作AE⊥CB,垂足为E.
∵∠ABC=120°,∴∠ABE=60°,在Rt△ABE中:AE=AB·sin60°=![]() ·
·![]() =
=![]()
∵PA⊥平面![]() ,AE⊥EB,∴AE是PE在平面
,AE⊥EB,∴AE是PE在平面![]() 内的射影,
内的射影,
∴PE⊥EB,∴PE为点P到BC的距离.在Rt△PAE中:PE=![]() .
.
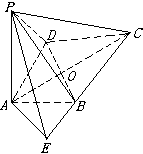
(2)在四边形ABCD中,取BD中点O,连AO、CO,
∵AB=AD,CD=CB,BO=OD,
∴AO⊥BD,CO⊥BD,
∴A、O、C共线,∴AC⊥BD.
又PA⊥![]() ,∴PA⊥BD,
,∴PA⊥BD,
∴BD⊥平面PAC,∵BD![]() 平面PBD,
平面PBD,
∴平面PBD⊥平面PAC.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 如图,已知平面四边形ABCD中,△BCD为正三角形,AB=AD=2,∠BAD=2θ,记四边形ABCD的面积为S.
如图,已知平面四边形ABCD中,△BCD为正三角形,AB=AD=2,∠BAD=2θ,记四边形ABCD的面积为S.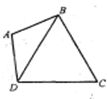 如图,已知平面四边形ABCD中,△BCD为正三角形,AB=AD=2,∠BAD=2θ,记四边形ABCD的面积为S.
如图,已知平面四边形ABCD中,△BCD为正三角形,AB=AD=2,∠BAD=2θ,记四边形ABCD的面积为S.