题目内容
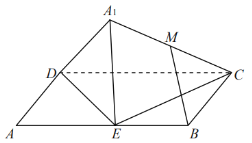
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 为边
为边![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻折成
翻折成![]() ,设
,设![]() 为线段
为线段![]() 的中点.则在
的中点.则在![]() 翻折过程中,给出如下结论:
翻折过程中,给出如下结论:
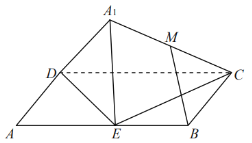
①当![]() 不在平面
不在平面![]() 内时,
内时,![]() 平面
平面![]() ;
;
②存在某个位置,使得![]() ;
;
③线段![]() 的长是定值;
的长是定值;
④当三棱锥![]() 体积最大时,其外接球的表面积为
体积最大时,其外接球的表面积为![]() .
.
其中,所有正确结论的序号是______.(请将所有正确结论的序号都填上)
【答案】①③④
【解析】
①取DC的中点N,连接NM、NB,;MN∥A1D,NB∥DE,所以面MNB∥面A1DE,所以MB∥面A1DE;
②用反证法,假设存在某个位置,使DE⊥A1C,在△CDE中,由勾股定理易知,CE⊥DE,再由线面垂直的判定定理可知,DE⊥面A1CE,所以DE⊥A1E,与已知相矛盾;
③由①可知,可得MN、NB和∠MNB均为定值,在△MNB中,由余弦定理可知,MB2=MN2+NB2﹣2MNNBcos∠MNB,所以线段BM的长是定值;
④当体积最大时,平面![]() 平面
平面![]() ,可得
,可得![]() 平面
平面![]() ,设外接球球心为
,设外接球球心为![]() ,半径为
,半径为![]() ,根据球的性质可知
,根据球的性质可知![]() ,即可求出半径,计算球的表面积.
,即可求出半径,计算球的表面积.
①取DC的中点N,连接NM、NB,如图,
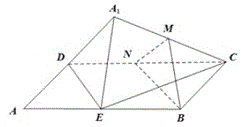
则MN∥A1D,NB∥DE,且MN∩NB=N,A1D∩DE=D,所以面MNB∥面A1DE,所以MB∥面A1DE,即①正确;
且MN=![]() =定值;NB∥DE,且NB=DE=定值,所以∠MNB=∠A1DE=定值,
=定值;NB∥DE,且NB=DE=定值,所以∠MNB=∠A1DE=定值,
②假设存在某个位置,使DE⊥A1C.由AB=2AD=2,∠BAD=60°可求得DE=1,![]() ,所以CE2+DE2=CD2,即CE⊥DE,因为A1C∩CE=C,所以DE⊥面A1CE,因为A1E面A1CE,所以DE⊥A1E,与已知相矛盾,即②错误;
,所以CE2+DE2=CD2,即CE⊥DE,因为A1C∩CE=C,所以DE⊥面A1CE,因为A1E面A1CE,所以DE⊥A1E,与已知相矛盾,即②错误;
③由①可知,MN∥A1D且MN=![]() =定值;NB∥DE,且NB=DE=定值,所以∠MNB=∠A1DE=定值,由余弦定理得,MB2=MN2+NB2﹣2MNNBcos∠MNB,所以BM的长为定值,即③正确;
=定值;NB∥DE,且NB=DE=定值,所以∠MNB=∠A1DE=定值,由余弦定理得,MB2=MN2+NB2﹣2MNNBcos∠MNB,所以BM的长为定值,即③正确;
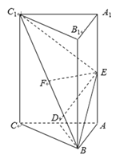
④当平面![]() 平面
平面![]() 时,三棱锥
时,三棱锥![]() 体积最大,此时因为
体积最大,此时因为![]() ,
,![]() 是平面
是平面![]() 与平面
与平面![]() 的交线,所以
的交线,所以![]() 平面
平面![]() ,设正三角形
,设正三角形![]() 中心为
中心为![]() ,棱锥外接球球心为
,棱锥外接球球心为![]() ,半径为
,半径为![]() ,则
,则![]() ,设
,设![]() 与
与![]() 交于
交于![]() ,连接
,连接![]() ,
,![]() ,如图:
,如图:
易知![]() ,
,![]() ,由题意可知
,由题意可知![]() 为边长为1的等边三角形,
为边长为1的等边三角形,![]() ,
,
则有![]() ,
,![]() ,
,

所以![]() ,故球的表面积为
,故球的表面积为![]() ,即④正确.
,即④正确.
故答案为:①③④.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案【题目】为了调查某社区居民每天参加健身的时间,某机构在该社区随机采访男性、女性各50名,其中每人每天的健身时间不少于1小时称为“健身族”,否则称其为"非健身族”,调查结果如下:
健身族 | 非健身族 | 合计 | |
男性 | 40 | 10 | 50 |
女性 | 30 | 20 | 50 |
合计 | 70 | 30 | 100 |
(1)若居民每人每天的平均健身时间不低于70分钟,则称该社区为“健身社区”. 已知被随机采访的男性健身族,男性非健身族,女性健身族,女性非健身族每人每天的平均健分时间分別是1.2小时,0.8小时,1.5小时,0.7小时,试估计该社区可否称为“健身社区”?
(2)根据以上数据,能否在犯错误的概率不超过5%的情况下认为“健身族”与“性别”有关?
参考公式: 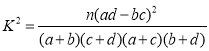 ,其中
,其中![]() .
.
参考数据:
| 0. 50 | 0. 40 | 0. 25 | 0. 05 | 0. 025 | 0. 010 |
| 0. 455 | 0. 708 | 1. 321 | 3. 840 | 5. 024 | 6. 635 |
【题目】某省即将实行新高考,不再实行文理分科.某校为了研究数学成绩优秀是否对选择物理有影响,对该校2018级的1000名学生进行调查,收集到相关数据如下:
(1)根据以上提供的信息,完成![]() 列联表,并完善等高条形图;
列联表,并完善等高条形图;
选物理 | 不选物理 | 总计 | |
数学成绩优秀 | |||
数学成绩不优秀 | 260 | ||
总计 | 600 | 1000 |
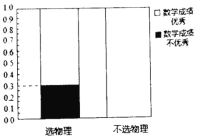
(2)能否在犯错误的概率不超过0.05的前提下认为数学成绩优秀与选物理有关?
附: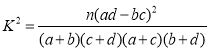
临界值表:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |