题目内容
6.已知sinα=$\frac{4\sqrt{3}}{7}$,cos(β-α)=$\frac{13}{14}$,且0<α<β<$\frac{π}{2}$.(1)求tan2α值;
(2)求cosβ值.
分析 (1)根据题意求得tanα的值,进而利用正切的二倍角公式求得答案.
(2)求得cosα和sin(β-α)的值,进而利用两角和与差的余弦函数公式求得答案.
解答 解:(1)∵0<α<β<$\frac{π}{2}$,
∴0<β-α$<\frac{π}{2}$,
∴tanα=4$\sqrt{3}$,tan(β-α)=$\frac{3\sqrt{3}}{13}$,
∴tan2α=$\frac{2tanα}{1-ta{n}^{2}α}$=$\frac{8\sqrt{3}}{1-48}$=-$\frac{8\sqrt{3}}{47}$.
(2)由(1)可知cosα=$\frac{1}{7}$,sin(β-α)=$\frac{3\sqrt{3}}{14}$
cosβ=cos(α+β-α)=cosαcos(β-α)-sinαsin(β-α)=$\frac{1}{7}$×$\frac{13}{14}$-$\frac{4\sqrt{3}}{7}$×$\frac{3\sqrt{3}}{14}$=-$\frac{23}{98}$.
点评 本题主要考查了两角和与差的正切函数,同角三角函数基本关系的应用.考查了学生对基础公式的熟练应用.

练习册系列答案
相关题目
16.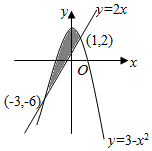 如图,阴影部分的面积是( )
如图,阴影部分的面积是( )
 如图,阴影部分的面积是( )
如图,阴影部分的面积是( )| A. | 2$\sqrt{3}$ | B. | -2$\sqrt{3}$ | C. | $\frac{32}{3}$ | D. | $\frac{35}{3}$ |
17.函数y=sinx-$\sqrt{3}$cosx的图象的一条对称轴方程是( )
| A. | x=$\frac{π}{6}$ | B. | x=$\frac{π}{3}$ | C. | x=$\frac{2π}{3}$ | D. | x=$\frac{5π}{6}$ |
15.设函数f(x)=sinωπx(ω>0)的图象在区间[0,$\frac{1}{2}$]上有两个最高点和一个最低点,则( )
| A. | 3≤ω<5 | B. | 4≤ω<6 | C. | 5≤ω<7 | D. | 6≤ω<8 |
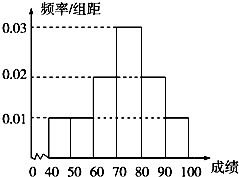 某校举办安全法规知识竞赛,从参赛的高一、高二学生中各抽出100人的成绩作为样本.对高一年级的100名学生的成绩进行统计,得到成绩分布的频率分布直方图如图:
某校举办安全法规知识竞赛,从参赛的高一、高二学生中各抽出100人的成绩作为样本.对高一年级的100名学生的成绩进行统计,得到成绩分布的频率分布直方图如图: