题目内容

11．函数f（x）=$\sqrt{{x}^{2}-6x+13}$+$\sqrt{{x}^{2}+4x+5}$的最小值为$\sqrt{34}$．

分析 由配方可得函数表示f（x）表示P（x，0）到两点A（3，2），B（-2，1）的距离之和．作出点A关于x轴的对称点A'（3，-2），连接A'B，交x轴于P，运用两点之间线段最短，由两点的距离公式计算即可得到．

解答 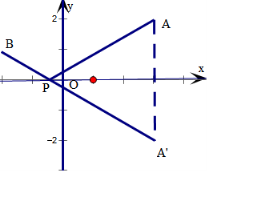解：函数f（x）=$\sqrt{{x}^{2}-6x+13}$+$\sqrt{{x}^{2}+4x+5}$
=$\sqrt{（x-3）^{2}+{2}^{2}}$+$\sqrt{（x+2）^{2}+{1}^{2}}$，
设点P（x，0），A（3，2），B（-2，1），
则f（x）表示P到两点A，B的距离之和．
作出点A关于x轴的对称点A'（3，-2），
连接A'B，交x轴于P，
则||PA|+|PB|=|PA'|+|PB|≥|A'B|=$\sqrt{25+9}$=$\sqrt{34}$，
则当A，P，B'三点共线，取得最小值$\sqrt{34}$．

点评 本题考查函数的最值的求法，注意运用几何方法：对称法，两点间的距离公式，属于中档题．

练习册系列答案
相关题目
1．已知f（x）=lnx-$\frac{1}{x}$，g（x）=ax+b．若函数h（x）=f（x）-g（x）在（0，+∞）上单调递增，求实数a的取值范围．
2．已知函数f（x）=$\sqrt{2}$sinωx（ω＞0）相邻两个最值点的横坐标之差的绝对值为$\frac{π}{2}$，其图象上所有点向左平移$\frac{π}{8}$个单位得到g（x）的图象，若x∈（0，$\frac{π}{4}$）．则g（x）的值域为（-1，1）．
19．求证：
（1）对任意的x∈R，都有ex≥x+1；
（2）对任意的∈（0，+∞），都有$\frac{x-1}{x}$≤lnx．
6．y=sin（ωx+$\frac{π}{6}$）（ω＞0）在区间[-$\frac{3π}{4}$，$\frac{π}{2}$]上不单调，则ω的取值范围（　　）
A．（0，$\frac{2}{3}$）B．（$\frac{2}{3}$，+∞）C．（0，$\frac{2}{3}$]D．[$\frac{2}{3}$，+∞）
16．已知函数f（x）=sin2x+2sin（$\frac{π}{4}$+x）cos（$\frac{π}{4}$+x），x∈R．
（1）求f（$\frac{π}{4}$）的值；
（2）求函数f（x）的最小正周期；
（3）求函数f（x）的最小值及此时x的集合．
3．设?＞0，x≤t≤y，|x-a|＜?，|y-a|＜?，求证：|t-a|＜?．
20．已知定点M（0，2），N（-2，0），直线l：kx-y-2k+2=0（k为常数）．
（Ⅰ）若点M，N到直线l的距离相等，求实数k的值；
（Ⅱ）以M，N为直径的圆与直线l相交所得的弦长为2，求实数k的值．
1．用数学归纳法证明某命题时，左式为$\frac{1}{2}$+cosα+cos3α+…+cos（2n-1）α（α≠kπ，k∈Z，n∈N*）在验证n=1时，左边所得的代数式为（　　）
A．$\frac{1}{2}$B．$\frac{1}{2}$+cosα
C．$\frac{1}{2}$+cosα+cos3αD．$\frac{1}{2}$+cosα+cos3α+cos5α

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网