题目内容
18.从装有n+1个球(其中n个白球,1个黑球)的口袋中取出m个球(0<m≤n,m,n∈N),共有$C_{n+1}^m$种取法.在这$C_{n+1}^m$种取法中,可以分成两类:一类是取出的m个球全部为白球,共有$C_1^0•C_n^m$种取法;另一类是取出的m个球有m-1个白球和1个黑球,共有$C_1^1•C_n^{m-1}$种取法.显然$C_1^0•C_n^m+C_1^1•C_n^{m-1}=C_{n+1}^m$,即有等式:$C_n^m+C_n^{m-1}=C_{n+1}^m$成立.试根据上述思想化简下列式子:$C_n^m+C_k^1C_n^{m-1}+C_k^2C_n^{m-2}+…+C_k^k•C_n^{m-k}$=Cn+km.分析 从装有n+1个球(其中n个白球,1个黑球)的口袋中取出m个球(0<m≤n,m,n∈N),共有Cn+1m种取法.在这Cn+1m种取法中,可以分成两类:一类是取出的m个球全部为白球,另一类是,取出1个黑球,m-1个白球,则Cnm+Cnm-1=Cn+1m根据上述思想,在式子:Cnm+Ck1•Cnm-1+Ck2•Cnm-2+…+Ckk•Cnm-k中,从第一项到最后一项分别表示:从装有n个白球,k个黑球的袋子里,取出m个球的所有情况取法总数的和,故答案应为:从从装有n+k球中取出m个球的不同取法数,根据排列组合公式,易得答案.
解答 解:在Cnm+Ck1•Cnm-1+Ck2•Cnm-2+…+Ckk•Cnm-k中,
从第一项到最后一项分别表示:
从装有n个白球,k个黑球的袋子里,
取出m个球的所有情况取法总数的和,
故答案应为:从从装有n+k球中取出m个球的不同取法数Cn+km
故答案为:Cn+km.
点评 这个题结合考查了推理和排列组合,处理本题的关键是熟练掌握排列组合公式,明白每一项所表示的含义,再结合已知条件进行分析,最后给出正确的答案.

练习册系列答案
相关题目
11.已知向量$\overrightarrow{a}$=(-1,2),$\overrightarrow{b}$=(2,x),若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则实数x等于( )
| A. | 1 | B. | -1 | C. | -4 | D. | 4 |
10.已知i是虚数单位,z=1+i,则复数$\frac{1}{z}$在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
6.已知命题p:?x∈R,2x2+1>0,则¬p是( )
| A. | ?x∈R,2x2+1≤0 | B. | ?x0∈R,2x02+1>0 | C. | ?x0∈R,2x02+1<0 | D. | ?x0∈R,2x02+1≤0 |
13.甲、乙两人从4门课程中各选修2门,则甲、乙所选的课程中至少有1门不相同的概率等于( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
6.已知数列{an}满足a1=0,an+1=$\frac{{{a_n}-2}}{{\frac{5}{4}{a_n}-2}}$,则a2015=( )
| A. | 0 | B. | 1 | C. | $\frac{4}{3}$ | D. | 2 |
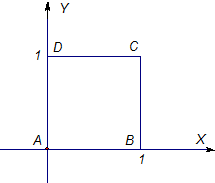 如图,在直角坐标系中,正方形ABCD的四个顶点分别为A(0,0),B(1,0),C(1,1),D(0,1).
如图,在直角坐标系中,正方形ABCD的四个顶点分别为A(0,0),B(1,0),C(1,1),D(0,1).