题目内容
1.已知异面直线a,b成60°角,P为空间一点,则过P且与a,b所成角均为45°,60°,80°的直线有( )| A. | 1,2,3条 | B. | 2,2,4条 | C. | 2,3,4条 | D. | 1,3,3条 |
分析 过P作a′∥a,b′∥b,设直线a′、b′确定的平面为α,异面直线a、b成60°角,直线a′、b′所成锐角为60°,进而可得满足条件的直线的条数.
解答 解:过P作a′∥a,b′∥b,
设直线a′、b′确定的平面为α,
∵异面直线a、b成60°角,
∴直线a′、b′所成锐角为60°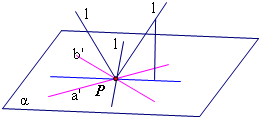
①当直线l在平面α内时,
若直线l平分直线a′、b′所成的钝角,
则直线l与a、b都成60°角;
②当直线l与平面α斜交时,
若它在平面α内的射影恰好落在
直线a′、b′所成的锐角平分线上时,直线l与a、b所成角相等.
此时l与a′、b′所成角的范围为[30°,90°],
适当调整l的位置,可使直线l与a、b也都成60°角,这样的直线l有两条.
综上所述,过点P与a′、b′都成60°角的直线,可以作3条
∵a′∥a,b′∥b,
∴过点P与a′、b′都成60°角的直线,与a、b也都成60°的角.
同理,过P且与a,b所成角均为45°的直线有2条,
过P且与a,b所成角均为80°的直线有4条,
故选:C
点评 本题考查满足条件的直线有多少条的判断,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.已知m1+i=1-ni,其中m,n∈R,i为虚数单位,则m+ni( )
| A. | 2+i | B. | 1+2i | C. | 1-i | D. | 1-2i |