题目内容
15.设Q是曲线T:xy=2(x>0)上任意一点,l是曲线T在点Q处的切线,且l交坐标轴于A,B两点,O为坐标原点,则△OAB的面积为4.分析 设Q(x0,y0)为曲线T:y=$\frac{2}{x}$(x>0)上任一点,过点Q作曲线C的切线l,利用导数可求得切线l的斜率及方程,从而可求得l与两坐标轴交于A,B两点的坐标,继而可求△OAB的面积.
解答 解:设Q(x0,y0)为曲线T:y=$\frac{2}{x}$(x>0)上任一点,则y0=$\frac{2}{{x}_{0}}$.
设过曲线C:y=$\frac{2}{x}$上一点Q的切线l的斜率为k,
∵y′=-$\frac{2}{{x}^{2}}$,∴k=-$\frac{2}{{{x}_{0}}^{2}}$,
∴切线l的方程为:y-y0=-$\frac{2}{{{x}_{0}}^{2}}$(x-x0),
∴当x=0时,y=$\frac{2}{{x}_{0}}$+y0=$\frac{4}{{x}_{0}}$,即B(0,$\frac{4}{{x}_{0}}$);
当y=0时,x=y0•x02+x0=2x0,即A(2x0,0);
∴S△OAB=$\frac{1}{2}$|OA|•|OB|=$\frac{1}{2}$×|2x0|•|$\frac{4}{{x}_{0}}$|=4.
故答案为:4.
点评 本题考查利用导数求过曲线T:xy=2(x>0)上一点Q的切线l的斜率,考查直线的方程及截距,考查三角形的面积公式,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
6.某中学一名数学老师对全班50名学生某次考试成绩分男女进行了统计(满分150分),得到右面频率分布表:其中120分(含120分)以上为优秀.
(1)根据以上频率表的数据,完成下面的2×2列联表:
(2)根据(1)中表格的数据计算,你有多大把握认为学生的数学成绩与性别之间的关系?
(3)若从成绩及在[130,140]的学生中任取3人,已知取到的第一个人是男生,求取到的另外2人中至少有1名女生的概率.
(1)根据以上频率表的数据,完成下面的2×2列联表:
(2)根据(1)中表格的数据计算,你有多大把握认为学生的数学成绩与性别之间的关系?
(3)若从成绩及在[130,140]的学生中任取3人,已知取到的第一个人是男生,求取到的另外2人中至少有1名女生的概率.
| 分组 | 频率 | |
| 男生 | 女生 | |
| [80,90] | 0 | 0.02 |
| [90,100] | 0.04 | 0.08 |
| [100,110] | 0.06 | 0.12 |
| [110,120] | 0.10 | 0.18 |
| [120,130] | 0.18 | 0.10 |
| [130,140] | 0.08 | 0.04 |
3.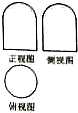 一个几何体的三视图如图,正视图和俯视图都是由一个边长为2的正方形组成,俯视图是一个圆,则这个几何体的表面积为( )
一个几何体的三视图如图,正视图和俯视图都是由一个边长为2的正方形组成,俯视图是一个圆,则这个几何体的表面积为( )
 一个几何体的三视图如图,正视图和俯视图都是由一个边长为2的正方形组成,俯视图是一个圆,则这个几何体的表面积为( )
一个几何体的三视图如图,正视图和俯视图都是由一个边长为2的正方形组成,俯视图是一个圆,则这个几何体的表面积为( )| A. | 5π | B. | 6π | C. | 7π | D. | 9π |
11.已知在数列{an}中,a1=1,当n≥2时,其前n项和Sn满足Sn2=an(Sn-$\frac{1}{2}$),则S2014的值为( )
| A. | 2014 | B. | 4027 | C. | $\frac{1}{4027}$ | D. | $\frac{1}{2014}$ |