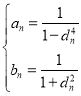题目内容
【题目】已知集合![]() ,集合
,集合![]() .
.
(1)若![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)是否存在实数![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)![]() ;(2)不存在,理由见解析.
;(2)不存在,理由见解析.
【解析】
试题分析:(1)因为![]() ,所以集合
,所以集合![]() 可以分为
可以分为![]() 或
或![]() 两种情况来讨论.当
两种情况来讨论.当![]() 时,
时,![]() ;当
;当![]() 时,得
时,得 .综上所述
.综上所述![]() ;(2)若存在实数
;(2)若存在实数![]() ,使
,使![]() ,则必有
,则必有![]() ,无解.故不存在.
,无解.故不存在.
试题解析:
(1)因为![]() ,所以集合
,所以集合![]() 可以分为
可以分为![]() 或
或![]() 两种情况来讨论;..........1分
两种情况来讨论;..........1分
当![]() 时,
时,![]() ....................2分
....................2分
当![]() 时,得
时,得 .......................5分
.......................5分
综上,![]() ................................6分
................................6分
(2)若存在实数![]() ,使
,使![]() ,则必有
,则必有![]() ,无解.
,无解.
故不存在实数![]() ,使
,使![]() .....................10分
.....................10分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某班同学利用国庆节进行社会实践,对![]() 岁的人群随机抽取
岁的人群随机抽取![]() 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低硕族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低硕族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 低碳族的人数 | 占本组的频率 |
第一组 |
| 120 | 0.6 |
第二组 |
| 195 |
|
第三组 |
| 100 | 0.5 |
第四组 |
|
| 0.4 |
第五组 |
| 30 | 0.3 |
第六组 |
| 15 | 0.3 |
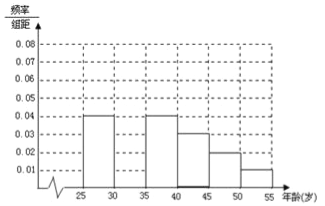
(1)补全频率分布直方图并求![]() 的值(直接写结果);
的值(直接写结果);
(2)从年龄段在![]() 的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中至少有1人年龄在
的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中至少有1人年龄在![]() 岁的概率.
岁的概率.