题目内容
选修4-4：坐标系与参数方程
在以坐标原点为极点，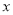
轴正半轴为极轴的极坐标系中，圆
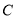的极坐标方程为：
.
（Ⅰ）将极坐标方程化为普通方程；
（Ⅱ）若点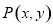
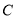在圆上，求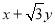
的取值范围.
练习册系列答案
芒果教辅达标测试卷系列答案
相关题目
芒果教辅达标测试卷系列答案题目内容
选修4-4：坐标系与参数方程
在以坐标原点为极点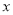，轴正半轴为极轴的极坐标系中，圆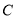的极坐标方程为：.
（Ⅰ）将极坐标方程化为普通方程；
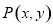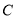（Ⅱ）若点在圆上，求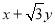的取值范围.
芒果教辅达标测试卷系列答案
是自然对数的底数.
在
上的单调性；
时，若存在
，使得
，求实数
的取值范围.（参考公式：
）
的值为
，则输出的
值为（ ）
B．
C．
D．
的右焦点为
，过点
作与
轴垂直的直线
交两渐近线于
，
两点，且与双曲线在第一象限的交点为
，设
为坐标原点，若
（
，
），
，则该双曲线的离心率为（ ）
B．
C．3 D．2
层楼时，上下楼造成的不满意度为
，但高处空气清新，嘈杂音较小，环境较为安静，因此随教室所在楼层升高，环境不满意度降低，设教室在第
层时楼，环境不满意度为
，则同学们认为最适宜的教室应在（ ）
的前
项和为
，且满足
，
.
，求
的前
.
的图象向左平移
个单位，再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变)，所得图象关于
对称，则
的最小值为（ ）
B.
D.
为数列
的前
项和，且满足
，则
；
.
中，椭圆
：
（
）的离心率是
，抛物线
：
的焦点
是
的一个顶点．
的方程；
是
上的动点，且位于第一象限，
在点
处的切线
与
交于不同的两点
，
，线段
的中点为
，直线
与过
且垂直于
轴的直线交于点
．
在定直线上；
与
轴交于点
，记△
的面积为
，△
的面积为
，求
的最大值及取得最大值时点
的坐标．