题目内容
A、B是治疗同一种疾病的两种药,用若干试验组进行对比试验。每个试验组由4只小白鼠组成,其中2只服用A,另2只服用B,然后观察疗效。若在一个试验组中,服用A有效的小白鼠的只数比服用B有效的多,就称该试验组为甲类组。设每只小白鼠服用A有效的概率为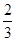 ,服用B有效的概率为
,服用B有效的概率为 。
。
(Ⅰ)求一个试验组为甲类组的概率;
(Ⅱ)观察3个试验组,用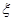 表示这3个试验组中甲类组的个数,求
表示这3个试验组中甲类组的个数,求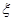 的分布列和数学期望。
的分布列和数学期望。
(1) P=P(B0·A1)+P(B0·A2)+P(B1·A2)= 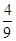 ;
;
(Ⅱ)ξ的分布列为: ξ 0 1 2 3 P 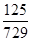
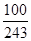
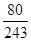
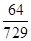
解析试题分析:(1)设Ai表示事件“一个试验组中,服用A有效的小鼠有i只" , i=0,1,2,
Bi表示事件“一个试验组中,服用B有效的小鼠有i只" , i="0,1,2,"
依题意有: P(A1)=2× ×
×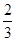 =
= 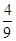 , P(A2)=
, P(A2)= 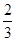 ×
×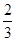 =
= 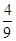 . P(B0)=
. P(B0)=  ×
× =
= 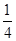 ,
,
P(B1)=2× ×
× =
=  , 所求概率为: P=P(B0·A1)+P(B0·A2)+P(B1·A2)
, 所求概率为: P=P(B0·A1)+P(B0·A2)+P(B1·A2)
= 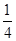 ×
×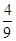 +
+ 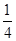 ×
×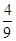 +
+  ×
×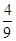 =
= 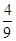
(Ⅱ)ξ的可能值为0,1,2,3且ξ~B(3, 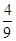 ) . P(ξ="0)=("
) . P(ξ="0)=(" 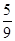 )3=
)3= 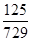 , P(ξ=1)=C31×
, P(ξ=1)=C31×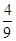 ×(
×(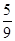 )2=
)2=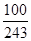 ,
,
P(ξ=2)=C32×(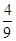 )2×
)2×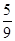 =
= 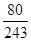 , P(ξ="3)=("
, P(ξ="3)=(" 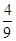 )3=
)3= 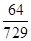
ξ的分布列为:
考点:本题主要考查离散性随机变量的分布列。ξ 0 1 2 3 P 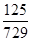
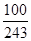
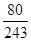
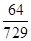
点评:典型题,利用概率知识解决实际问题,在高考题中常常出现,这类题目解答的难点在于求随机变量的概率。

 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案在某校高三学生的数学校本课程选课过程中,规定每位同学只能选一个科目。已知某班第一小组与第二小组各 有六位同学选择科目甲或科 目乙,情况如下表:
| | 科目甲 | 科目乙 | 总计 |
| 第一小组 | 1 | 5 | 6 |
| 第二小组 | 2 | 4 | 6 |
| 总计 | 3 | 9 | 12 |
(1)求选出的4 人均选科目乙的概率;
(2)设
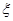 为选出的4个人中选科目甲的人数,求
为选出的4个人中选科目甲的人数,求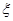 的分布列和数学期望.
的分布列和数学期望. (本小题满分12分)某品牌的汽车4S店,对最近100位采用分期付款的购车者进行统计,统计结果如下表所示:已知分3期付款的频率为0.2,4S店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元,分2期或3期付款其利润为1.5万元;分4期或5期付款,其利润为2万元,用 表示经销一辆汽车的利润。
表示经销一辆汽车的利润。
| 付款方工 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频数 | 40 | 20 |  | 10 |  |
 值;(2)若以频率作为概率,求事件A:“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的频率P(A);(3)求
值;(2)若以频率作为概率,求事件A:“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的频率P(A);(3)求 的分布列及数学期望E
的分布列及数学期望E 。
。 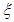 为检测出不合格产品的听数,求
为检测出不合格产品的听数,求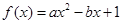 ,分别从集合P和Q中随机取一个数a和b得到数列
,分别从集合P和Q中随机取一个数a和b得到数列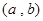 。
。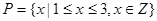 ,
,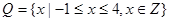 ,列举出所有的数对
,列举出所有的数对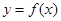 有零点的概率;
有零点的概率;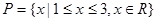 ,
,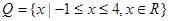 ,求函数
,求函数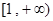 上是增函数的概率。
上是增函数的概率。 的
的 ,已知
,已知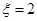 时,共有6种坐法.
时,共有6种坐法.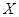 ,求
,求 .
. ,满足
,满足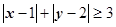 电脑显示“中奖”,且抽奖者获得9000元奖金;否则电脑显示“谢谢”,则不中奖.
电脑显示“中奖”,且抽奖者获得9000元奖金;否则电脑显示“谢谢”,则不中奖.