题目内容
【题目】已知椭圆![]() :
:![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,过点
,过点![]() 的直线
的直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,
两点,![]() 的周长为
的周长为![]() ,
, ![]() 的离心率
的离心率![]()
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)设点![]() ,
,![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,试判断直线
,试判断直线![]() 与直线
与直线![]() 的交点是否恒在一条定直线上?若是,求该定直线的方程;否则,说明理由.
的交点是否恒在一条定直线上?若是,求该定直线的方程;否则,说明理由.
【答案】(I)![]() ;(II)
;(II)![]() .
.
【解析】
(I)由![]() 的周长为
的周长为![]() 求得椭圆的a,再离心率
求得椭圆的a,再离心率![]() ,然后求得椭圆的方程;
,然后求得椭圆的方程;
(II)设直线l:x=my+4,![]() ,联立方程,运用韦达定理,再写出直线BD的方程为:
,联立方程,运用韦达定理,再写出直线BD的方程为:![]() 与
与![]() 的交点,最后求解计算出
的交点,最后求解计算出![]() 与m无关,得出答案.
与m无关,得出答案.
解:(I)由椭圆的定义,![]() 的周长为
的周长为![]() ,即4a=20,解得a=5,
,即4a=20,解得a=5,
又椭圆![]() 的离心率
的离心率![]() ,解得c=4
,解得c=4
所以![]()
所以椭圆方程![]() ;
;
(II)显然过点![]() 的直线l不垂直y轴,设l:x=my+4,
的直线l不垂直y轴,设l:x=my+4,![]()
联立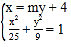 ,得
,得![]()
韦达定理:![]()
直线![]() 的方程为
的方程为![]()
直线BD的方程为:![]()
解得![]()
又点![]() 在直线l上,所以
在直线l上,所以![]()
再代入解得![]()
又![]()
代入解得 (与m无关)
(与m无关)
故直线![]() 与直线BD的交点恒落在直线
与直线BD的交点恒落在直线![]() 上.
上.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目