题目内容
【题目】以![]() 为直径的圆上每一点都染上了红、黄、蓝三色之一,已知
为直径的圆上每一点都染上了红、黄、蓝三色之一,已知![]() 、
、![]() 染上了红色,联结圆上的点组成三角形,给出4个结论:
染上了红色,联结圆上的点组成三角形,给出4个结论:
①必定存在一个直角三角形,三个顶点同为红色;
②必定存在一个直角三角形,三个顶点同色;
③必定存在一个直角三角形,三个顶点全不同色;
④必定存在一个直角三角形,或都三个顶点同色,或者三个顶点全不同色。
则真命题的个数是( )个。
A. 1 B. 2
C. 3 D. 4
【答案】A
【解析】
易知,联结圆上的点组成直角三角形,当且仅当斜边为直径,下面讨论直径.若除点![]() 、
、![]() 外,圆上再无红点,则结论①不成立;若除点
外,圆上再无红点,则结论①不成立;若除点![]() 、
、![]() 外,圆上再无红点,且其他所有直径的两端点都黄、蓝异色,则结论②不成立;若圆上所有直径的两端点都同色,则结论③不成立.下面证明:结论④成立.若除点
外,圆上再无红点,且其他所有直径的两端点都黄、蓝异色,则结论②不成立;若圆上所有直径的两端点都同色,则结论③不成立.下面证明:结论④成立.若除点![]() 、
、![]() 外,圆上还有红点,则存在三个顶点同色的直角三角形(同红色),命题成立,若除点
外,圆上还有红点,则存在三个顶点同色的直角三角形(同红色),命题成立,若除点![]() 、
、![]() 外,圆上再无红点(即圆上其余点染上了黄、蓝两色之一),则作直径
外,圆上再无红点(即圆上其余点染上了黄、蓝两色之一),则作直径![]() ,当
,当![]() 两端异色时,存在三个顶点全不同色的直角三角形,命题成立;当
两端异色时,存在三个顶点全不同色的直角三角形,命题成立;当![]() 两端同色时,不妨记为同黄色,若此时圆上还有第三个黄点,则存在三个顶点同黄色的直角三角形,命题成立.若此时圆上没有第三个黄点,即除点
两端同色时,不妨记为同黄色,若此时圆上还有第三个黄点,则存在三个顶点同黄色的直角三角形,命题成立.若此时圆上没有第三个黄点,即除点![]() 、
、![]() 、
、![]() 、
、![]() 外圆上全为蓝点,则存在三个顶点同蓝色的直角三角形,命题成立。综上得结论④成立。
外圆上全为蓝点,则存在三个顶点同蓝色的直角三角形,命题成立。综上得结论④成立。

【题目】为了调查观众对电影“复仇者联盟4”结局的满意程度,研究人员在某电影院随机抽取了1000名观众作调查,所得结果如下所示,其中不喜欢“复仇者联盟4”的结局的观众占被调查观众总数的![]() .
.
男性观众 | 女性观众 | 总计 | |
喜欢“复仇者联盟4”的结局 | 400 | ||
不喜欢“复仇者联盟4”的结局 | 200 | ||
总计 |
(Ⅰ)完善上述![]() 列联表;
列联表;
(Ⅱ)是否有99.9%的把握认为观众对电影“复仇者联盟4”结局的满意程度与性别具有相关性?
附: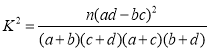
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |


