��Ŀ����
����Ŀ������һ���ڼ䣬Ϊ���������������������ij����������˾��Ͷ��һ��������������������������100��������A��B�����ͺŵĵ���������A�ͳ�Ϊ�˶��ͣ��ɱ�Ϊ400Ԫ![]() �������а�Сʱ�軨��
�������а�Сʱ�軨��![]() Ԫ��B�ͳ�Ϊ����ͣ��ɱ�Ϊ2400Ԫ
Ԫ��B�ͳ�Ϊ����ͣ��ɱ�Ϊ2400Ԫ![]() �������а�Сʱ�軨��1Ԫ
�������а�Сʱ�軨��1Ԫ![]() ����˾Ͷ��ɱ��ʽ��ܳ���8��Ԫ����Ͷ��ij���ƽ��ÿ��ÿ��ᱻ����2�Σ�ÿ�β�������Сʱ
����˾Ͷ��ɱ��ʽ��ܳ���8��Ԫ����Ͷ��ij���ƽ��ÿ��ÿ��ᱻ����2�Σ�ÿ�β�������Сʱ![]() �����Сʱ����Сʱ����
�����Сʱ����Сʱ����![]() ���ʹ�˾���Ͷ�������ͺŵĵ�������ʹÿ���õ���������࣬���Ϊ����Ԫ��
���ʹ�˾���Ͷ�������ͺŵĵ�������ʹÿ���õ���������࣬���Ϊ����Ԫ��
���𰸡���˾Ͷ�������ͺŵĵ����ֱ�Ϊ80��20������ʹÿ���õ���������࣬���Ϊ120Ԫ��
��������
�������⣬��Ͷ��A�ͺŵ���x����B�ͺŵ���y����������˾�ɻ�õ�������ΪZ���ɵõ�Լ��������ʽ�ӣ���Ŀ�꺯��![]() ����������ʽ���ʾ��ƽ������Ŀ�꺯��
����������ʽ���ʾ��ƽ������Ŀ�꺯��![]() ��������
��������![]() ʱ��
ʱ��![]() ȡ�����ֵ����⼴�ɡ�
ȡ�����ֵ����⼴�ɡ�
�⣺�������⣬��Ͷ��A�ͺŵ���x����B�ͺŵ���y����������˾ÿ��ɻ�õ�������ΪZ��
����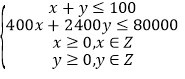 ��
��
��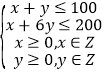 ��
��![]()
��![]() ��
��
��������ʽ��![]() ��ʾ��ƽ��������
��ʾ��ƽ��������![]() �����
�����![]() .
.
��Ŀ�꺯��![]() ��������
��������![]() ʱ��
ʱ��![]() ȡ�����ֵΪ��
ȡ�����ֵΪ��![]() .
.

�𣺹�˾Ͷ�������ͺŵĵ����ֱ�Ϊ80��20������ʹÿ���õ���������࣬���Ϊ120Ԫ��

 �ǻۿ����ܾ�100�ֵ�Ԫ���ؼ��ϵ�д�
�ǻۿ����ܾ�100�ֵ�Ԫ���ؼ��ϵ�д� ��Ԫ������ĩ��ϵ�д�
��Ԫ������ĩ��ϵ�д�����Ŀ����������1��2��3��![]() ��n��
��n��![]() �ų����������ʾ������һ��3�������ڶ���6�������Һ�һ�б�ǰһ�ж�3����������i�У���j�е�������
�ų����������ʾ������һ��3�������ڶ���6�������Һ�һ�б�ǰһ�ж�3����������i�У���j�е�������![]() ��ʾ����100�ɱ�ʾΪ______��
��ʾ����100�ɱ�ʾΪ______��
��1�� | ��2�� | ��3�� | ��4�� | ��5�� | ��6�� | ��7�� | ��8�� |
| |
��1�� | 1 | 2 | 3 | ||||||
��2�� | 9 | 8 | 7 | 6 | 5 | 4 | |||
��3�� | 10/p> | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
|
|