题目内容
在平面直角坐标系xOy中,椭圆C: =1(a>b>0)的右焦点为F(4m,0)(m>0,m为常数),离心率等于0.8,过焦点F、倾斜角为θ的直线l交椭圆C于M、N两点.
=1(a>b>0)的右焦点为F(4m,0)(m>0,m为常数),离心率等于0.8,过焦点F、倾斜角为θ的直线l交椭圆C于M、N两点.

(1)求椭圆C的标准方程;
(2)若θ=90°, ,求实数m;
,求实数m;
(3)试问 的值是否与θ的大小无关,并证明你的结论.
的值是否与θ的大小无关,并证明你的结论.
 =1(a>b>0)的右焦点为F(4m,0)(m>0,m为常数),离心率等于0.8,过焦点F、倾斜角为θ的直线l交椭圆C于M、N两点.
=1(a>b>0)的右焦点为F(4m,0)(m>0,m为常数),离心率等于0.8,过焦点F、倾斜角为θ的直线l交椭圆C于M、N两点.
(1)求椭圆C的标准方程;
(2)若θ=90°,
 ,求实数m;
,求实数m;(3)试问
 的值是否与θ的大小无关,并证明你的结论.
的值是否与θ的大小无关,并证明你的结论.(1)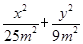 =1.(2)m=
=1.(2)m= (3)无关
(3)无关
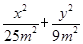 =1.(2)m=
=1.(2)m= (3)无关
(3)无关(1)∵c=4m,椭圆离心率e=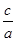 =
=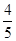 ,∴a=5m.∴b=3m.
,∴a=5m.∴b=3m.
∴椭圆C的标准方程为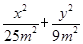 =1.
=1.
(2)在椭圆方程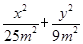 =1中,令x=4m,解得y=±
=1中,令x=4m,解得y=±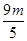 .
.
∵当θ=90°时,直线MN⊥x轴,此时FM=FN=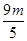 ,∴
,∴ =
=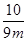 .
.
∵ =
=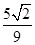 ,∴
,∴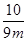 =
=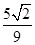 ,解得m=
,解得m=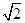 .
.
(3) 的值与θ的大小无关.
的值与θ的大小无关.
证明如下:(证法1)设点M、N到右准线的距离分别为d1、d2.
∵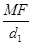 =
=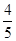 ,
,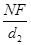 =
=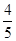 ,∴
,∴ =
=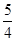
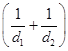 .
.
又由图可知,MFcosθ+d1=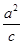 -c=
-c=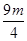 ,
,
∴d1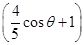 =
=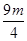 ,即
,即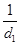 =
=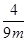
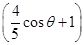 .
.
同理,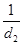 =
=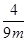
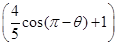 =
=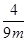 (-
(-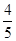 cosθ+1).
cosθ+1).
∴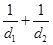 =
=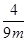
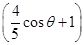 +
+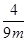 (-
(-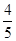 cosθ+1)=
cosθ+1)=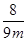 .
.
∴ =
=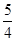 ·
·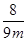 =
=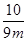 .显然该值与θ的大小无关.
.显然该值与θ的大小无关.
(证法2)当直线MN的斜率不存在时,由(2)知, 的值与θ的大小无关.
的值与θ的大小无关.
当直线MN的斜率存在时,设直线MN的方程为y=k(x-4m),
代入椭圆方程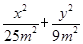 =1,得(25k2+9)m2x2-200m3k2x+25m4(16k2-9)=0.
=1,得(25k2+9)m2x2-200m3k2x+25m4(16k2-9)=0.
设点M(x1,y1)、N(x2,y2),∵Δ>0恒成立,∴x1+x2=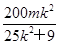 ,x1·x2=
,x1·x2=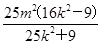 .
.
∵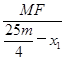 =
=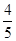 ,
,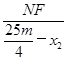 =
=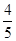 ,∴MF=5m-
,∴MF=5m-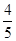 x1,NF=5m-
x1,NF=5m-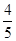 x2.
x2.
∴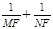 =
=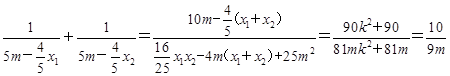 .
.
显然该值与θ的大小无关.
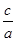 =
=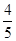 ,∴a=5m.∴b=3m.
,∴a=5m.∴b=3m.∴椭圆C的标准方程为
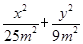 =1.
=1.(2)在椭圆方程
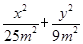 =1中,令x=4m,解得y=±
=1中,令x=4m,解得y=±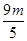 .
.∵当θ=90°时,直线MN⊥x轴,此时FM=FN=
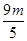 ,∴
,∴ =
=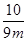 .
.∵
 =
=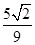 ,∴
,∴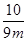 =
=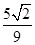 ,解得m=
,解得m=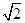 .
.(3)
 的值与θ的大小无关.
的值与θ的大小无关.证明如下:(证法1)设点M、N到右准线的距离分别为d1、d2.
∵
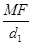 =
=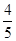 ,
,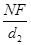 =
=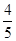 ,∴
,∴ =
=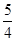
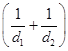 .
.又由图可知,MFcosθ+d1=
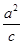 -c=
-c=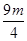 ,
,∴d1
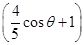 =
=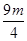 ,即
,即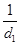 =
=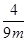
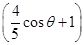 .
.同理,
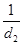 =
=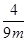
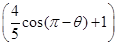 =
=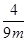 (-
(-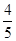 cosθ+1).
cosθ+1).∴
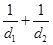 =
=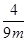
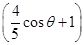 +
+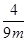 (-
(-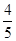 cosθ+1)=
cosθ+1)=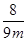 .
.∴
 =
=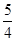 ·
·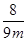 =
=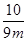 .显然该值与θ的大小无关.
.显然该值与θ的大小无关.(证法2)当直线MN的斜率不存在时,由(2)知,
 的值与θ的大小无关.
的值与θ的大小无关.当直线MN的斜率存在时,设直线MN的方程为y=k(x-4m),
代入椭圆方程
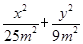 =1,得(25k2+9)m2x2-200m3k2x+25m4(16k2-9)=0.
=1,得(25k2+9)m2x2-200m3k2x+25m4(16k2-9)=0.设点M(x1,y1)、N(x2,y2),∵Δ>0恒成立,∴x1+x2=
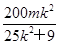 ,x1·x2=
,x1·x2=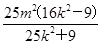 .
.∵
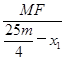 =
=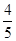 ,
,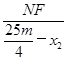 =
=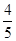 ,∴MF=5m-
,∴MF=5m-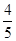 x1,NF=5m-
x1,NF=5m-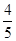 x2.
x2.∴
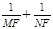 =
=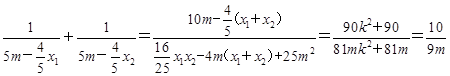 .
.显然该值与θ的大小无关.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 :
: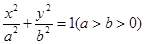 ,称圆心在原点
,称圆心在原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆 ,其短轴上的一个端点到
,其短轴上的一个端点到 的距离为
的距离为 .
.
 是椭圆
是椭圆 交“准圆”于点
交“准圆”于点 .
. 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线 ;
; 的长为定值.
的长为定值. =1(a>b>0)的左、右顶点与上顶点,直线A2B与圆C:x2+y2=1相切.
=1(a>b>0)的左、右顶点与上顶点,直线A2B与圆C:x2+y2=1相切. =1;
=1; ,求椭圆E的方程;
,求椭圆E的方程; ·
· =0,试判断直线l与圆C的位置关系,并说明理由.
=0,试判断直线l与圆C的位置关系,并说明理由. 的两焦点在
的两焦点在 轴上, 且两焦点与短轴的一个顶点的连线构成斜边长为2的等腰直角三角形
轴上, 且两焦点与短轴的一个顶点的连线构成斜边长为2的等腰直角三角形 的动直线
的动直线 交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点Q,使得以AB为直径的圆恒过点Q?若存在求出点Q的坐标;若不存在,请说明理由
交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点Q,使得以AB为直径的圆恒过点Q?若存在求出点Q的坐标;若不存在,请说明理由  ,且
,且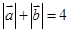 .
.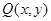 的轨迹
的轨迹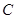 的方程;
的方程;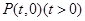 ,若斜率为
,若斜率为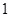 的直线
的直线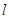 过点
过点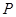 并与轨迹
并与轨迹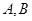 ,且对于轨迹
,且对于轨迹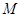 ,都存在
,都存在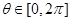 ,使得
,使得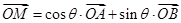 成立,试求出满足条件的实数
成立,试求出满足条件的实数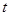 的值.
的值. 与
与 的曲线大致是( )
的曲线大致是( )
 =1(a>b>0)的一个顶点为A(2,0),离心率为
=1(a>b>0)的一个顶点为A(2,0),离心率为 .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N. 时,求k的值.
时,求k的值. ,
, 是双曲线
是双曲线 :
: 与椭圆
与椭圆 的公共焦点,点
的公共焦点,点 是
是 ,
, 在第一象限的公共点.若|F1F2|=|F1A|,则
在第一象限的公共点.若|F1F2|=|F1A|,则



