题目内容
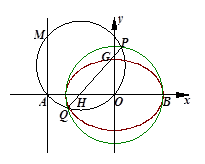
已知圆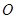 :
: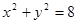 交
交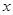 轴于
轴于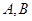 两点,曲线
两点,曲线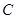 是以
是以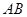 为长轴,直线:
为长轴,直线: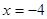 为准线的椭圆.
为准线的椭圆.
(1)求椭圆的标准方程;
(2)若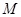 是直线上的任意一点,以
是直线上的任意一点,以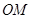 为直径的圆
为直径的圆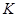 与圆
与圆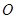 相交于
相交于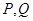 两点,求证:直线
两点,求证:直线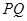 必过定点
必过定点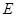 ,并求出点
,并求出点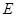 的坐标;
的坐标;
(3)如图所示,若直线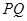 与椭圆
与椭圆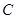 交于
交于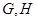 两点,且
两点,且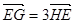 ,试求此时弦
,试求此时弦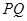 的长.
的长.
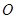 :
: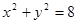 交
交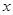 轴于
轴于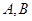 两点,曲线
两点,曲线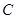 是以
是以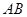 为长轴,直线:
为长轴,直线: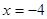 为准线的椭圆.
为准线的椭圆.
(1)求椭圆的标准方程;
(2)若
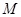 是直线上的任意一点,以
是直线上的任意一点,以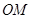 为直径的圆
为直径的圆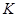 与圆
与圆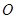 相交于
相交于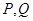 两点,求证:直线
两点,求证:直线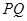 必过定点
必过定点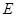 ,并求出点
,并求出点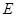 的坐标;
的坐标;(3)如图所示,若直线
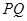 与椭圆
与椭圆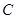 交于
交于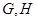 两点,且
两点,且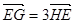 ,试求此时弦
,试求此时弦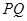 的长.
的长.(1)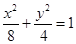 (2)
(2)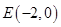 (3)
(3)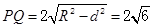
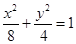 (2)
(2)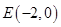 (3)
(3)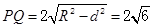
试题分析:解:(Ⅰ)设椭圆的标准方程为
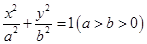 ,则:
,则: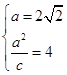 ,从而:
,从而: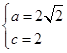 ,故
,故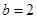 ,所以椭圆的标准方程为
,所以椭圆的标准方程为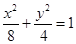 。 4分
。 4分(Ⅱ)设
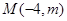 ,则圆
,则圆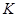 方程为
方程为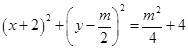
与圆
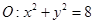 联立消去
联立消去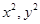 得
得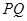 的方程为
的方程为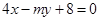 ,
, 过定点
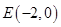 。 …………8分
。 …………8分 (Ⅲ)解法一:设
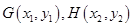 ,则
,则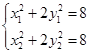 ,………①
,………① 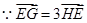 ,
,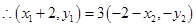 ,即:
,即: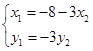
代入①解得:
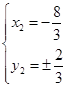 (舍去正值),
(舍去正值), 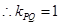 ,所以
,所以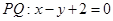 ,
,从而圆心
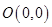 到直线
到直线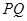 的距离
的距离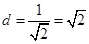 ,从而,
,从而,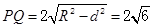 16分
16分点评:解决直线与圆锥曲线的位置关系的时候,一般采用联立方程组的思想来得到,属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
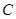 的极坐标方程是
的极坐标方程是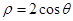 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为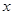 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线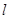 的参数方程为
的参数方程为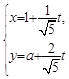 (
(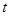 为参数).若直线
为参数).若直线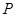 ,
,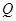 两点,且
两点,且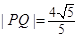 .
.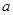 的值.
的值. 相切, 则△AOB的面积最小值为_____________.
相切, 则△AOB的面积最小值为_____________. 与圆
与圆 相交于
相交于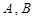 两点,且
两点,且 则
则 的值是
的值是 


 轴相切的圆的方程是( )
轴相切的圆的方程是( ) 



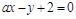 与圆
与圆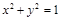 相切,则实数
相切,则实数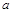 的值为 .
的值为 . 上到直线
上到直线 的距离为
的距离为 的点数共有________个。
的点数共有________个。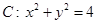 ,直线
,直线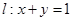 ,则圆C内任意一点到直线的距离小于
,则圆C内任意一点到直线的距离小于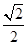 的概率为( )
的概率为( )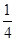
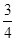
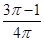
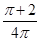
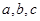 是直角三角形的三边(
是直角三角形的三边(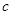 为斜边), 则圆
为斜边), 则圆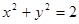 被直线
被直线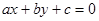 所截得的弦长等于__________.
所截得的弦长等于__________.