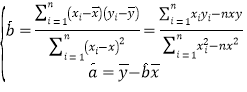题目内容
【题目】定义在![]() 上的函数
上的函数![]() ,
,![]() 单调递增,
单调递增,![]() ,若对任意
,若对任意![]() ,存在
,存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 是
是![]() 在
在![]() 上的“追逐函数”.若
上的“追逐函数”.若![]() ,则下列四个命题:①
,则下列四个命题:①![]() 是
是![]() 在
在![]() 上的“追逐函数”;②若
上的“追逐函数”;②若![]() 是
是![]() 在
在![]() 上的“追逐函数”,则
上的“追逐函数”,则![]() ;③
;③![]() 是
是![]() 在
在![]() 上的“追逐函数”;④当
上的“追逐函数”;④当![]() 时,存在
时,存在![]() ,使得
,使得![]() 是
是![]() 在
在![]() 上的“追逐函数”.其中正确命题的个数为( )
上的“追逐函数”.其中正确命题的个数为( )
A. ①③B. ②④C. ①④D. ②③
【答案】B
【解析】
由题意,分析每一个选项,首先判断单调性,以及![]() ,再假设是
,再假设是
“追逐函数”,利用题目已知的性质,看是否满足,然后确定答案.
对于①,可得![]() ,
,![]() 在
在![]() 是递增函数,
是递增函数,![]() ,若
,若![]() 是
是![]() 在
在![]() 上的“追逐函数”;则
上的“追逐函数”;则![]() 存在
存在![]() ,使得
,使得![]() 成立,即
成立,即![]() ,此时当k=100时,不存在
,此时当k=100时,不存在![]() ,故①错误;
,故①错误;
对于②,若![]() 是
是![]() 在
在![]() 上的“追逐函数”,此时
上的“追逐函数”,此时![]() ,解得
,解得
![]() ,当
,当![]() 时,
时,![]() ,
,![]() 在
在![]() 是递增函数,若是“追逐函数”
是递增函数,若是“追逐函数”
则![]() ,即
,即![]() ,
,
设函数![]()
即![]() ,则存在
,则存在![]() ,所以②正确;
,所以②正确;
对于③![]() ,
,![]() 在
在![]() 是递增函数,
是递增函数,![]() ,若
,若![]() 是
是![]() 在
在![]() 上的“追逐函数”;则
上的“追逐函数”;则![]() 存在
存在![]() ,使得
,使得![]() 成立,即
成立,即![]() ,当k=4时,就不存在
,当k=4时,就不存在![]() ,故③错误;
,故③错误;
对于④,当t=m=1时,就成立,验证如下:
![]() ,
,![]() 在
在![]() 是递增函数,
是递增函数,![]() ,若
,若![]() 是
是![]() 在
在![]() 上的“追逐函数”;则
上的“追逐函数”;则![]() 存在
存在![]() ,使得
,使得![]() 成立,
成立,
即![]() 此时
此时![]()
取![]()
即![]() ,故存在存在
,故存在存在![]() ,所以④正确;
,所以④正确;
故选B

练习册系列答案
相关题目
【题目】某种设备随着使用年限的增加,每年的维护费相应增加.现对一批该设备进行调查,得到这批设备自购入使用之日起,前5年平均每台设备每年的维护费用大致如表:
年份 |
|
|
|
|
|
维护费 |
|
|
|
|
|
(I)从这![]() 年中随机抽取两年,求平均每台设备每年的维护费用至少有
年中随机抽取两年,求平均每台设备每年的维护费用至少有![]() 年多于
年多于![]() 万元的概率;
万元的概率;
(II)求![]() 关于
关于![]() 的线性回归方程;若该设备的价格是每台
的线性回归方程;若该设备的价格是每台![]() 万元,你认为应该使用满五年换一次设备,还是应该使用满八年换一次设备?并说明理由.
万元,你认为应该使用满五年换一次设备,还是应该使用满八年换一次设备?并说明理由.
参考公式:用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式: