题目内容
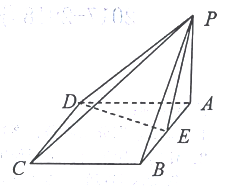
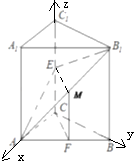
【题目】如图,已知直三棱柱ABC﹣A1B1C1中,∠ACB=90°,E是棱CC1上的动点,F是AB的中点,AC=BC=2,AA1=4.
(1)当E是棱CC1的中点时,求证:CF∥平面AEB1;
(2)在棱CC1上是否存在点E,使得二面角A﹣EB1﹣B的大小是45°?若存在,求出CE的长,若不存在,请说明理由.
【答案】
(1)解:取AB1中点M,连接EM、FM
∵△AB1B中,M、F分别是AB、AB1的中点,
∴MF∥B1B且MF= ![]() B1B,
B1B,
又∵矩形BB1C1C中,CE∥B1B且CE= ![]() B1B,
B1B,
∴MF∥CE且MF=CE,可得四边形MFCE是平行四边形
∴CF∥EM
∵CF平面EAB1,EM平面EAB1,
∴CF∥平面AEB1
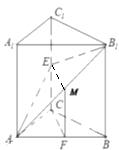
(2)解:以CA、CB、CC1为x、y、z轴,建立如图空间直角坐标系,
可得A(2,0,0),B1(0,2,4),设CE=m,得E(0,0,m)
∴ ![]() =(﹣2,0,m),
=(﹣2,0,m), ![]() =(﹣2,2,4)
=(﹣2,2,4)
设平面AEB1的法向量为 ![]() =(x,y,z)
=(x,y,z)
则有 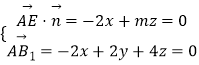 ,解之并取z=2,得
,解之并取z=2,得 ![]() =(m,m﹣4,2)
=(m,m﹣4,2)
∵平面EB1B的法向量为 ![]() =(2,0,0),
=(2,0,0),
∴当二面角A﹣EB1﹣B的大小是45°时,有
cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() ,解之得m=
,解之得m= ![]() .
.
因此,在棱CC1上存在点E,当CE= ![]() 时,二面角A﹣EB1﹣B的大小是45°.
时,二面角A﹣EB1﹣B的大小是45°.
【解析】(1)根据题意作出辅助线,由已知条件可得线线平行进而得出直线与平面平行。(2)根据题意建立空间直角坐标系,分别求出各个点以及向量的坐标,设出平面AEB1的法向量再根据法向量和向量AE的数量积等于零求出法向量的坐标,再根据数量积的运算公式结合二面角A﹣EB1﹣B的大小求出余弦值进而得到m的值,即可得证点E的存在。
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案