题目内容
【题目】已知两条直线![]() :
:![]() 和
和![]() :
:![]() ,试分别确定
,试分别确定![]() 、
、![]() 的值,使:
的值,使:
(1)![]() ;
;
(2)![]() 且
且![]() 在
在![]() 轴上的截距为
轴上的截距为![]() .
.
【答案】解 (1)当m=0时,显然l1与l2不平行.
当m≠0时,由=≠得
m·m-8×2=0,得m=±4,
8×(-1)-n·m≠0,得n≠±2,
即m=4,n≠-2时,或m=-4,n≠2时,l1∥l2.------------6分
(2)当且仅当m·2+8·m=0,即m=0时,l1⊥l2.
又-=-1,∴n=8.
即m=0,n=8时,l1⊥l2,且l1在y轴上的截距为-1.--------------12分
【解析】
试题(1)本题考察的是两直线平行的判定,若![]() 平行,只需
平行,只需![]() ,根据已知条件代入相应的数值即可求出
,根据已知条件代入相应的数值即可求出![]() 的值.
的值.
(2)本题考察的是两直线垂直的判断,若![]() 垂直,则
垂直,则![]() ,根据已知条件代入相应的数值即可求出
,根据已知条件代入相应的数值即可求出![]() 的值.
的值.
试题解析:(1)![]() ,
,![]() ,
,
解得![]() ,或
,或![]()
(2)由题得![]() ,解得
,解得![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某校进行文科、理科数学成绩对比,某次考试后,各随机抽取100名同学的数学考试成绩进行统计,其频率分布表如下.
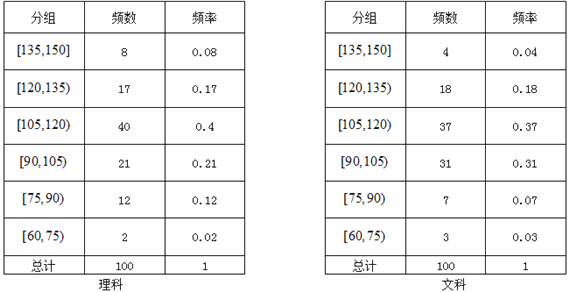
(Ⅰ)根据数学成绩的频率分布表,求理科数学成绩的中位数的估计值;
(Ⅱ)请填写下面的列联表,并根据列联表判断是否有90%的把握认为数学成绩与文理科有关:

(Ⅲ)设文理科数学成绩相互独立,记![]() 表示事件“文科、理科数学成绩都大于等于120分”,估计
表示事件“文科、理科数学成绩都大于等于120分”,估计![]() 的概率.
的概率.
附: 
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |