题目内容
给定两个命题, :对任意实数
:对任意实数 都有
都有 恒成立;
恒成立; :关于
:关于 的方程
的方程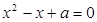 有实数根;如果
有实数根;如果 为真,
为真,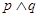 为假,求实数
为假,求实数 的取值范围.
的取值范围.

解析试题分析:根据二次函数恒成立的充要条件,我们可以求出命题p为真时,实数a的取值范围,根据二次函数有实根的充要条件,我们可以求出命题q为真时,实数a的取值范围,然后根据p∨q为真命题,p∧q为假命题,则命题p,q中一个为真一个为假,分类讨论后,即可得到实数a的取值范围.
试题解析:命题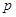 :对任意实数
:对任意实数 都有
都有 恒成立
恒成立
 3分
3分
命题 :关于
:关于 的方程
的方程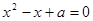 有实数根
有实数根
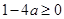 即
即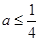 5分
5分
 为真,
为真,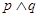 为假,
为假,
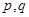 有且只有一个正确 7分
有且只有一个正确 7分
如果P正确,且q不正确,则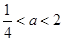 ; 9分
; 9分
如果q正确,且P不正确,则 . 11分
. 11分
所以实数 的取值范围为
的取值范围为 . 12分
. 12分
考点:1.复合命题的真假;2.函数恒成立问题.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
 :实数
:实数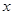 满足
满足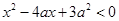 ,其中
,其中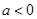 ,命题
,命题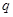 :实数
:实数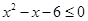 或
或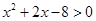 ,且
,且 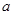 的取值范围.
的取值范围.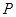 :复数
:复数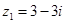 ,复数
,复数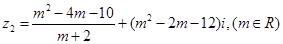 ,
, 是虚数;命题
是虚数;命题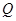 :关于
:关于 的方程
的方程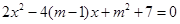 的两根之差的绝对值小于
的两根之差的绝对值小于 ;若
;若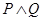 为真命题,求实数
为真命题,求实数 的取值范围.
的取值范围.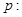 函数
函数 既有极大值又有极小值;
既有极大值又有极小值;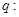 直线
直线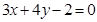 与圆
与圆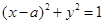 有公共点.
有公共点.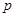 或
或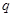 ”为真,且命题“
”为真,且命题“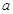 的取值范围.
的取值范围.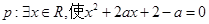 ;命题
;命题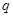 :不等式
:不等式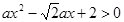 对任意
对任意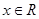 恒成立.若
恒成立.若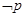 为真,且
为真,且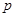 或
或 的取值范围.
的取值范围.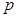 :不等式
:不等式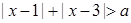 对一切实数
对一切实数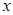 都成立;命题
都成立;命题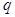 :已知函数
:已知函数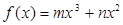 的图像在点
的图像在点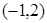 处的切线恰好与直线
处的切线恰好与直线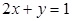 平行,且
平行,且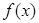 在
在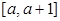 上单调递减.若命题
上单调递减.若命题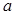 的取值范围.
的取值范围.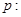 方程
方程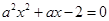 在
在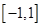 上有解,命题
上有解,命题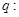 函数
函数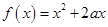
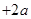 的值域为
的值域为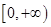 ,若命题“
,若命题“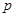 或
或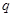 ”是假命题,求实数
”是假命题,求实数 的取值范围.
的取值范围.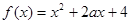 有零点;
有零点;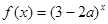 是增函数,
是增函数,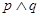 是真命题,求实数
是真命题,求实数 的取值范围.
的取值范围.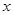 都有
都有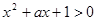 恒成立;命题q :关于
恒成立;命题q :关于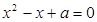 有实数根.若“p或q”为真命题,“p且q”为假命题,求实数
有实数根.若“p或q”为真命题,“p且q”为假命题,求实数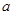 的取值范围。
的取值范围。