题目内容
【题目】如图所示,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
, ![]()
![]() 是线段
是线段![]() 的中垂线,
的中垂线,![]()
![]() ,
,![]() 为线段
为线段![]() 上的点.
上的点.

(Ⅰ)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 为
为![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成角的正切值;
所成角的正切值;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
【答案】(I)见解析;(II)![]() ;(III)
;(III)![]()
【解析】
(Ⅰ)根据线面垂直得线线垂直,再根据线线垂直得线面垂直,最后根据面面垂直判定定理得结论,(Ⅱ)先根据三角形中位线性质得线线平行,即得异面直线所成角的角或补角,再根据直角三角形求结果,(Ⅲ)作![]() ,根据线面垂直判定定理得
,根据线面垂直判定定理得![]() 面
面![]() ,即得线面角,最后根据直角三角形求结果.
,即得线面角,最后根据直角三角形求结果.
(Ⅰ)![]() 面
面![]() ,
,![]() 面
面![]()
![]()
又![]() ,
,![]() 面
面![]()
又![]() 面
面![]() 面
面![]() 面
面![]()
(II) 连结![]() ,
,![]() 分别为边
分别为边![]() 的中点,
的中点,![]()
![]()
![]() 为异面直线
为异面直线![]() 与
与![]() 所成角或其补角
所成角或其补角
在![]() 中,
中,![]()
![]()
所以异面直线![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]() .
.
(III) 连结![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,
,
由(I)可知![]() 面
面![]()
![]() 面
面![]()
![]() 面
面![]() 面
面![]() =
=![]()
![]() 面
面![]() 面
面![]() =
=![]()
![]() 面
面![]() ,
,![]() 为斜线
为斜线![]() 在面
在面![]() 内的射影,
内的射影,
![]() 为线
为线![]() 与面
与面![]() 所成角, 在
所成角, 在![]() 中,
中,![]()
![]() 直线
直线![]() 与面
与面![]() 所成角为
所成角为![]() .
.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
【题目】某小区为了调查居民的生活水平,随机从小区住户中抽取![]() 个家庭,得到数据如下:
个家庭,得到数据如下:
家庭编号 | 1 | 2 | 3 | 4 | 5 | 6 |
月收入x(千元) | 20 | 30 | 35 | 40 | 48 | 55 |
月支出y(千元) | 4 | 5 | 6 | 8 | 8 | 11 |
参考公式:回归直线的方程是:![]() ,其中,
,其中,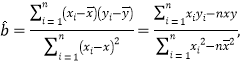
![]() .
.
(1)据题中数据,求月支出![]() (千元)关于月收入
(千元)关于月收入![]() (千元)的线性回归方程(保留一位小数);
(千元)的线性回归方程(保留一位小数);
(2)从这![]() 个家庭中随机抽取
个家庭中随机抽取![]() 个,求月支出都少于
个,求月支出都少于![]() 万元的概率.
万元的概率.
