题目内容
【题目】若函数![]() 为奇函数,且
为奇函数,且![]() 时
时![]() 有极小值
有极小值![]() .
.
(1)求实数![]() 的值;
的值;
(2)求实数![]() 的取值范围;
的取值范围;
(3)若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)1;(2)![]() ;(3)
;(3)![]()
【解析】
(1)计算![]() ,根据奇函数得到
,根据奇函数得到![]() 解得答案.
解得答案.
(2)![]() ,讨论
,讨论![]() 和
和![]() 两种情况,得到函数的单调区间和极值,计算得到答案.
两种情况,得到函数的单调区间和极值,计算得到答案.
(3)根据题意![]() ,令
,令![]() ,求导得到
,求导得到![]() 时
时![]() 单调递减,令
单调递减,令![]() ,则
,则![]() ,
,![]() ,得到答案.
,得到答案.
(1)由函数![]() 为奇函数可得
为奇函数可得![]() ,则
,则![]() ,
,![]() ,则
,则![]() ,
,
此时![]() ,对任意
,对任意![]() ,
,![]() ,
,
满足![]() 为奇函数,
为奇函数,![]() ;
;
(2)![]() ,
,
①![]() 时,由
时,由![]() ,可得
,可得![]() ,则
,则![]() ,仅当
,仅当![]() 时可能为0,
时可能为0,
则![]() 在
在![]() 上单调递增,无极小值;
上单调递增,无极小值;
②![]() 时,
时,![]() ,令
,令![]() ,可得
,可得![]() ,则
,则![]() ,
,
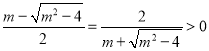 ,
,![]() ,
,
即![]() ,
,![]() ,则
,则![]() 的解为
的解为![]() ,
,![]() 单调性如下表:
单调性如下表:
|
|
|
|
| + | - | + |
| 递增 | 递减 | 递增 |
则![]() 在
在![]() 处取得极小值,即
处取得极小值,即![]() ,满足题意;
,满足题意;
综上,![]() 的取值范围是
的取值范围是![]() ;
;
(3)根据第二问可得![]() ,
,
则![]() ,
,
令![]() ,
,![]() ,
,
则![]() 时
时![]() 单调递减,
单调递减,
由![]() ,
,![]() ,
,![]() ,可得
,可得![]() ,
,
令![]() ,则
,则![]() ,
,![]() 在
在![]() 单调递增,则
单调递增,则![]() 的取值范围是
的取值范围是![]() .
.

【题目】为响应“文化强国建设”号召,并增加学生们对古典文学的学习兴趣,雅礼中学计划建设一个古典文学熏陶室.为了解学生阅读需求,随机抽取200名学生做统计调查.统计显示,男生喜欢阅读古典文学的有64人,不喜欢的有56人;女生喜欢阅读古典文学的有36人,不喜欢的有44人.
(1)能否在犯错误的概率不超过0.25的前提下认为喜欢阅读古典文学与性别有关系?
(2)为引导学生积极参与阅读古典文学书籍,语文教研组计划牵头举办雅礼教育集团古典文学阅读交流会.经过综合考虑与对比,语文教研组已经从这200人中筛选出了5名男生代表和4名女生代表,其中有3名男生代表和2名女生代表喜欢古典文学.现从这9名代表中任选3名男生代表和2名女生代表参加交流会,记![]() 为参加交流会的5人中喜欢古典文学的人数,求
为参加交流会的5人中喜欢古典文学的人数,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
附: ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 |
【题目】某牛奶厂要将一批牛奶用汽车从所在城市甲运至城市乙,已知从城市甲到城市乙只有两条公路,且运费由厂商承担.若厂商恰能在约定日期(×月×日)将牛奶送到,则城市乙的销售商一次性支付给牛奶厂20万元;若在约定日期前送到,每提前一天销售商将多支付给牛奶厂1万元;若在约定日期后送到,每迟到一天销售商将少支付给牛奶厂1万元.为保证牛奶新鲜度,汽车只能在约定日期的前两天出发,且只能选择其中的一条公路运送牛奶,已知下表内的信息:
统计信息 | 在不堵车的情况下到达城市乙所需时间(天) | 在堵车的情况下到达城市乙所需时间(天) | 堵车的概率 | 运费(万元) |
公路1 | 2 | 3 |
| 1.6 |
公路2 | 1 | 4 |
| 0.8 |
(1)记汽车选择公路1运送牛奶时牛奶厂获得的毛收入为![]() (单位:万元),求
(单位:万元),求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(2)如果你是牛奶厂的决策者,你选择哪条公路运送牛奶有可能让牛奶厂获得的毛收入更多?
(注:毛收入=销售商支付给牛奶厂的费用-运费)