题目内容
9.(1)从集合{0,1,2,3}中任取一个数x,从集合{0,1,2}中任取一个数y,求x>y的概率.(2)从区间[0,3]中任取一个数x,从区间[0,2]中任取一个数y,求x>y的概率.
分析 (1)从集合{0,1,2,3}中任取一个数x,从集合{0,1,2}中任取一个数y,根据古典概型的概率公式即可求x>y的概率.
(2)从区间[0,3]中任取一个数x,从区间[0,2]中任取一个数y,则$\left\{\begin{array}{l}{0≤x≤3}\\{0≤y≤2}\end{array}\right.$,求出对应的面积,利用几何概型的概率公式进行计算.
解答 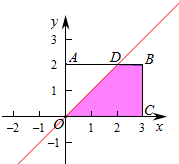 解:(1)从集合{0,1,2,3}中任取一个数x,从集合{0,1,2}中任取一个数y,共有4×3=12种,
解:(1)从集合{0,1,2,3}中任取一个数x,从集合{0,1,2}中任取一个数y,共有4×3=12种,
若x=3,则y=0,1,2,
若x=2,则y=0,1,
若x=1,则y=0,共有6种,
此时x>y的概率为P=$\frac{6}{12}=\frac{1}{2}$.
(2)从区间[0,3]中任取一个数x,从区间[0,2]中任取一个数y,
则$\left\{\begin{array}{l}{0≤x≤3}\\{0≤y≤2}\end{array}\right.$,对应的区域为矩形,
作出不等式组对应的平面区域如图:
则D(2,2),△OAD的面积S=$\frac{1}{2}×2×2=2$,
则阴影部分的面积S=3×2-2=4,
则从区间[0,3]中任取一个数x,从区间[0,2]中任取一个数y,x>y的概率的概率P=$\frac{4}{6}=\frac{2}{3}$.
点评 本题主要考查古典概型和几何概型的概率的计算,根据相应的公式是解决本题的关键.

练习册系列答案
相关题目
20.函数y=tan(sin x)的值域为( )
| A. | [-$\frac{π}{4}$,$\frac{π}{4}$] | B. | [-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$] | C. | [-tan 1,tan 1] | D. | 以上均不对 |
14.某大型企业人力资源部位研究企业员工工作积极性和对待企业改革态度的关系,随机抽取了180名员工进行调查,所得数据如下表所示:
对于人力资源部的研究项目,根据上述数据判断能否在犯错误的概率不超过0.5%的情况下认为工作积极和支持企业改革有关系.
附公式及相关数据:
k2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$(其中n=a+b+c+d).
| 支持企业改革 | 不支持企业改革 | 合计 | |
| 工作积极 | 50 | 40 | 90 |
| 工作不积极 | 30 | 60 | 90 |
| 总计 | 80 | 100 | 180 |
附公式及相关数据:
| P(k2≥k0) | 0.50 | 0.05 | 0.005 |
| k0 | 0.455 | 3.841 | 7.879 |
1.已知p:|x|<3,q:x2-x-2<0,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
18.若集合A={n|$\frac{{3}^{n}+{4}^{n}}{5}$∈N*,n∈N*},集合B={x|x=(2k-1)2+1,k∈N*},则集合A与B的关系为( )
| A. | B?A | B. | A?B | C. | A⊆B | D. | A=B |
19.集合A={x|x2-2x+1>0},B={x||x|<1},则A∩B=( )
| A. | (0,1) | B. | (-1,0)∪(0,1) | C. | (-1,1) | D. | (-∞,-1)∪(1,+∞) |