题目内容
11.设F1,F2分别为椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦分别为F1,F2,右顶点为A,上顶点为B,P为椭圆上在第一象限内一点,S${\;}_{△P{F}_{1}{F}_{2}}$,S${\;}_{△PA{F}_{2}}$,S${\;}_{△PB{F}_{1}}$分别为△PF1F2,△PAF2,△PBF1的面积,若S${\;}_{△P{F}_{1}{F}_{2}}$=S${\;}_{△PA{F}_{2}}$=S${\;}_{△PB{F}_{1}}$,则直线PF1的斜率为$\frac{2\sqrt{2}}{3}$.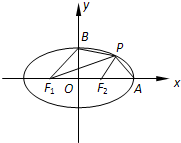
分析 通过设P(x,y),利用四边形F1BPA的面积S=${S}_{△BO{F}_{1}}$+S四边形BOAP=3${S}_{△PA{F}_{2}}$计算、整理可知bc+bx+ay=3(a-c)y,通过S${\;}_{△P{F}_{1}{F}_{2}}$=S${\;}_{△PA{F}_{2}}$可知a=3c,进而可知b=$2\sqrt{2}$c,代入计算、化简可知y=$\frac{2\sqrt{2}}{3}$(x+c),从而可得结论.
解答 解:依题意设P(x,y),则x>0、y>0,
则四边形F1BPA的面积S=${S}_{△BO{F}_{1}}$+S四边形BOAP
=$\frac{1}{2}$bc+$\frac{1}{2}$bx+$\frac{1}{2}$ay
=3${S}_{△PA{F}_{2}}$
=3×$\frac{1}{2}$×(a-c)y,
即bc+bx+ay=3(a-c)y,
又∵S${\;}_{△P{F}_{1}{F}_{2}}$=S${\;}_{△PA{F}_{2}}$,即点F2为线段AF1的中点,
∴2c=a-c,即a=3c,
∴b2=a2-c2=8c2,即b=$2\sqrt{2}$c,
代入bc+bx+ay=3(a-c)y,得$2\sqrt{2}$c2+$2\sqrt{2}$cx+3cy=6cy,
化简得:y=$\frac{2\sqrt{2}}{3}$(x+c),
∴直线PF1的斜率为$\frac{2\sqrt{2}}{3}$,
故答案为:$\frac{2\sqrt{2}}{3}$.
点评 本题考查椭圆的简单性质,考查运算求解能力,利用三角形的面积公式是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
1.在某次测量中得到的 A样本数据如下:582,584,584,586,586,586,588,588,588,588.
若B样本数据恰好是 A样本数据都加20后所得数据,则 A,B两样本的下列数字特征对应相同的是( )
若B样本数据恰好是 A样本数据都加20后所得数据,则 A,B两样本的下列数字特征对应相同的是( )
| A. | 众数 | B. | 平均数 | C. | 中位数 | D. | 标准差 |
16.设f(x),g(x)在(-∞,+∞)内有定义,f(x)为连续函数,且f(x)≠0,g(x)有间断点,下列函数中必有间断点的为( )
| A. | g[f(x)] | B. | [g(x)]2 | C. | f[g(x)] | D. | $\frac{g(x)}{f(x)}$ |
3.f(x)=log${\;}_{\frac{1}{2}}$${\;}^{3{x}^{2}-ax+5}$在[-1,+∞)单调递减,则a的取值范围为( )
| A. | (-∞,-6] | B. | (-8,-6] | C. | (-8,-6) | D. | [-6,+∞) |
1.动圆M经过点A(3,0)且与直线l:x=-3相切,则动圆圆心M的轨迹方程是( )
| A. | y2=12x | B. | y2=6x | C. | y2=3x | D. | y2=24x |