题目内容
(本小题满分12分)
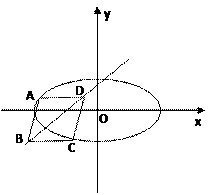
已知菱形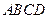 的顶点
的顶点 在椭圆
在椭圆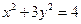 上,对角线
上,对角线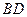 所在直线的斜率为1.
所在直线的斜率为1.
(1)当直线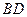 过点
过点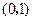 时,求直线
时,求直线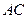
 的方程;
的方程;
(2)当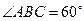 时,求菱形
时,求菱形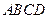 面积的最大值.
面积的最大值.

已知菱形
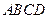 的顶点
的顶点 在椭圆
在椭圆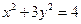 上,对角线
上,对角线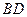 所在直线的斜率为1.
所在直线的斜率为1.(1)当直线
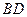 过点
过点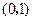 时,求直线
时,求直线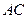
 的方程;
的方程;(2)当
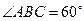 时,求菱形
时,求菱形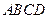 面积的最大值.
面积的最大值.(1)
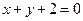
(2)

解:(1)由题意得直线
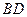 的方程为
的方程为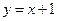 .因为四边形
.因为四边形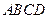 为菱形
为菱形 ,所以
,所以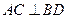 .
.于是可设直线
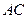 的方程为
的方程为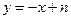 .
.由
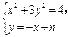 得
得 .
.因为
 在椭圆上,所以
在椭圆上,所以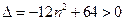 ,解得
,解得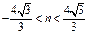 .
.设
 两点坐标分别为
两点坐标分别为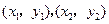 ,则
,则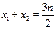 ,
,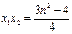 ,
,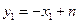 ,
,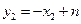 .所以
.所以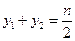 .所以
.所以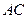 的中点坐标为
的中点坐标为 .
.由四边形
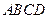 为菱形可知,点
为菱形可知,点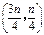 在直线
在直线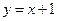 上, 所以
上, 所以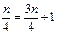 ,
,解得
 .所以直线
.所以直线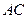 的方程为
的方程为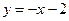 ,即
,即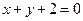 .
.(2)因为四边形
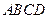 为菱形,且
为菱形,且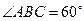 ,所以
,所以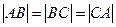 .
.所以菱形
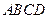 的面积
的面积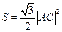 .
.由(1)可得
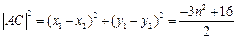 ,所以
,所以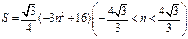 .
.所以当
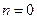 时,菱形
时,菱形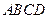 的面积取得最大值
的面积取得最大值 .
.
练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
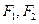 分别是椭圆
分别是椭圆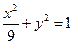 的左右焦点.
的左右焦点.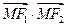 的最大值和最小值;
的最大值和最小值;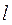 与椭圆交于不同的两点A、B,且
与椭圆交于不同的两点A、B,且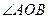
 为钝角,(其中O为坐标原点),求直线
为钝角,(其中O为坐标原点),求直线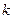 的取值范围。
的取值范围。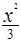 +
+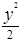 =1上一点P到左焦点的距离为
=1上一点P到左焦点的距离为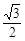 ,则P到右准线的距离为( )
,则P到右准线的距离为( )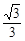
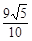

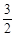
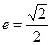 ,此椭圆与直线
,此椭圆与直线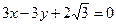 交于A、B两点,且OA⊥OB(其中O为坐标原点).
交于A、B两点,且OA⊥OB(其中O为坐标原点).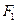 、
、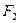 为椭圆的两个焦点,求
为椭圆的两个焦点,求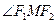 的取值范围;
的取值范围;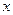 轴上,它的一个顶点恰好是抛物线
轴上,它的一个顶点恰好是抛物线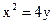 的焦点,离心率
的焦点,离心率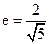 ,过椭圆的右焦点
,过椭圆的右焦点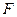 作不与坐标轴垂直的直线
作不与坐标轴垂直的直线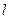 ,交椭圆于A、B两点.
,交椭圆于A、B两点.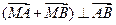 ,求
,求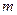 取值范围;
取值范围; 的方程为
的方程为 ,斜率为1的直线
,斜率为1的直线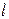 与椭圆
与椭圆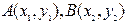 两点.
两点. ,直线
,直线 过点
过点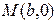 ,且
,且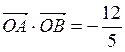 ,求椭圆
,求椭圆 的方程;
的方程; ,若点
,若点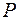 在椭圆
在椭圆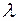 的取值范围.
的取值范围. 上一点,
上一点,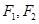 分别是左、右焦点,若
分别是左、右焦点,若 ,则
,则
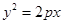 的焦点与椭圆
的焦点与椭圆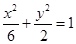 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( )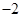
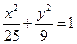
 的两个焦点, 过F1的直线交椭圆于A、B两点, 若
的两个焦点, 过F1的直线交椭圆于A、B两点, 若 , 则 |AB|=" "
, 则 |AB|=" "