题目内容
【题目】已知圆C的圆心C在直线![]() 上.
上.
![]() 若圆C与y轴的负半轴相切,且该圆截x轴所得的弦长为
若圆C与y轴的负半轴相切,且该圆截x轴所得的弦长为![]() ,求圆C的标准方程;
,求圆C的标准方程;
![]() 已知点
已知点![]() ,圆C的半径为3,且圆心C在第一象限,若圆C上存在点M,使
,圆C的半径为3,且圆心C在第一象限,若圆C上存在点M,使![]() 为坐标原点
为坐标原点![]() ,求圆心C的纵坐标的取值范围.
,求圆心C的纵坐标的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
![]() 根据圆心在直线
根据圆心在直线![]() 上,可设圆心
上,可设圆心![]() ,再根据圆C与y轴负半轴相切得
,再根据圆C与y轴负半轴相切得![]() ,弦长为
,弦长为![]() 列方程可解得
列方程可解得![]() ,从而可得圆C的标准方程;
,从而可得圆C的标准方程;
![]() 根据
根据![]() 可得点M的轨迹为圆
可得点M的轨迹为圆![]() ,记为圆D,再根据圆C和圆D有公共点列式可解得.
,记为圆D,再根据圆C和圆D有公共点列式可解得.
解:![]() 因为圆C的圆心在直线
因为圆C的圆心在直线![]() 上,所以可设圆心为
上,所以可设圆心为![]()
因为圆C与y轴的负半轴相切,所以![]() ,半径
,半径![]() ,
,
又因为该圆截学轴所得弦的弦长为![]() ,
,
所以![]() ,解得
,解得![]() ,
,
因此,圆心为![]() ,半径
,半径![]()
所以圆C的标准方程为![]()
![]() 圆C的半径为3,设圆C的圆心为
圆C的半径为3,设圆C的圆心为![]() ,由题意,
,由题意,![]()
则圆C的方程为![]()
又因为![]() ,
,![]() ,设
,设![]()
则![]() ,整理得
,整理得![]() ,
,
它表示以![]() 为圆心,2为半径的圆,记为圆D,
为圆心,2为半径的圆,记为圆D,
由题意可知:点M既在圆C上又在圆D上,即圆C和圆D有公共点.
所以![]() ,且
,且![]()
所以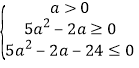 ,即
,即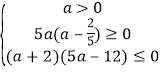 ,解得
,解得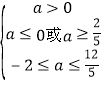 ,
,
解得![]()
所以圆心C的纵坐标的取值范围时![]()

练习册系列答案
相关题目

