题目内容
(本题满分14分)如图,AC 是圆 O 的直径,点 B 在圆 O 上,∠BAC=30°,BM⊥AC交 AC 于点 M,EA⊥平面ABC,FC//EA,AC=4,EA=3,FC=1.
(I)证明:EM⊥BF;
(II)求平面 BEF 与平面ABC 所成的二面角的余弦值.
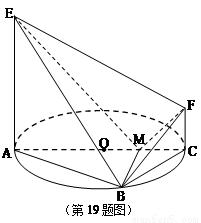

【答案】
解:
(1)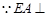 平面
平面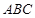 ,
,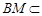 平面
平面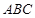 ,
,
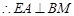 .
.
又 ,
,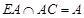 ,
,
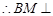 平面
平面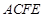
而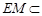 平面
平面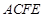
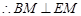 .
.
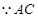 是圆
是圆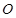 的直径,
的直径,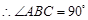 .
.
又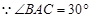 ,
,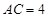 ,
,
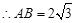 ,
,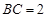 ,
,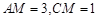 .
.
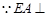 平面
平面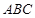 ,
,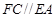 ,
,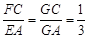 ,
,
 平面
平面 .
.
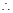
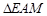 与
与 都是等腰直角三角形.
都是等腰直角三角形.
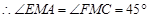 .
.
 ,即
,即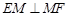 (也可由勾股定理证得).
(也可由勾股定理证得).
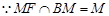 ,
,  平面
平面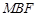 .
.
而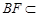 平面
平面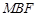 ,
,

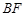 .
………………………………………………………………………………6分
.
………………………………………………………………………………6分
(2)延长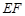 交
交 于
于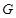 ,连
,连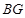 ,过
,过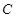 作
作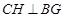 ,连结
,连结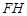 .
.
由(1)知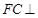 平面
平面 ,
, 平面
平面 ,
,
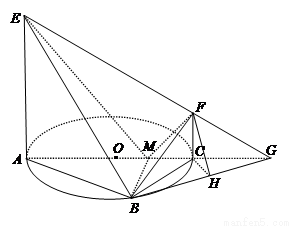
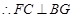 .
.
而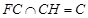 ,
,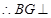 平面
平面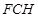 .
.
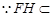 平面
平面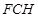 ,
,
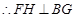 ,
,
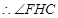 为平面
为平面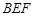 与平面
与平面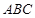 所成的
所成的
二面角的平面角. ……………………10分
在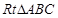 中,
中,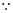
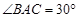 ,
,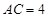 ,
,
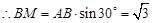 .
.
由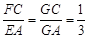 ,得
,得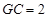 .
.
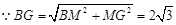 .
.
又 ,
,
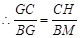 ,则
,则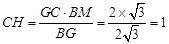 .[来源:学#科#网Z#X#X#K]
.[来源:学#科#网Z#X#X#K]
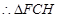 是等腰直角三角形,
是等腰直角三角形,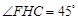 .[来源:Zxxk.Com]
.[来源:Zxxk.Com]
 平面
平面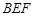 与平面
与平面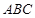 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为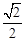 . ………………………14
. ………………………14
【解析】略

练习册系列答案
相关题目


 、
、 的边长都是1,平面
的边长都是1,平面 平面
平面 在
在 上移动,点
上移动,点 在
在 上移动,若
上移动,若 (
( )
)
 的长;
的长; 为何值时,
为何值时, 与面
与面 所成锐二面角余弦值的大小.
所成锐二面角余弦值的大小. ,又E、F分别是C1A和C1B的中点。
,又E、F分别是C1A和C1B的中点。 (1)求证:EF//平面ABC;
(1)求证:EF//平面ABC; 平面C1CBB1;
平面C1CBB1;