题目内容
【题目】已知动点P在抛物线x2=2y上,过点P作x轴的垂线,垂足为H,动点Q满足![]() .
.
(1)求动点O的轨迹E的方程;
(2)点M(-4,4),过点N(4,5)且斜率为k的直线交轨迹E于A,B两点,设直线MA,MB的斜率分别为k1,k2,求k1k2的值.
【答案】(1)x2=4y.(2)![]()
【解析】
(1)设点Q(x,y),由![]() ,则点P(x,2y),将点P坐标代入x2=2y中,得轨迹E的方程
,则点P(x,2y),将点P坐标代入x2=2y中,得轨迹E的方程
(2) )设过点N的直线方程为y=k(x-4)+5,A(x1,y1),B(x2,y2)联立方程,根据韦达定理得到关系式,再计算![]() ,化简得到答案.
,化简得到答案.
解:(1)设点Q(x,y),由![]() ,则点P(x,2y),
,则点P(x,2y),
因为P在x2=2y上,所以x2=2(2y),得轨迹E的方程为x2=4y.
(2)设过点N的直线方程为y=k(x-4)+5,A(x1,y1),B(x2,y2).
联立![]() 得x2-4kx+16k-20=0,则
得x2-4kx+16k-20=0,则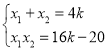 .
.
∵![]() ,∴
,∴![]() ,
,
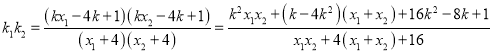
![]() .
.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目