题目内容
14．
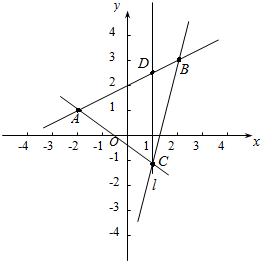已知点A（-2，1），B（2，3），C（1，-1），直线l经过点C且与线段AB相交，求直线l的斜率的取值范围．
分析 由题意可得kBC和kAC，由直线的倾斜角和斜率的关系数形结合可得．
解答 解：由题意可得kBC=$\frac{-1-3}{1-2}$=4，kAC=$\frac{-1-1}{1-（-2）}$=-$\frac{2}{3}$，
当直线l从CB开始逆时针旋转到与x轴垂直时，
直线的倾斜角增大（锐角），此时直线l的斜率k≥4，
当直线l从垂线继续旋转到AC时，
直线的倾斜角增大（钝角），此时直线l的斜率k≤-$\frac{2}{3}$，
综上可得直线l的斜率的取值范围为（-∞，-$\frac{2}{3}$]∪[4，+∞）
点评 本题考查简单线性规划，涉及直线的斜率和倾斜角的关系，属中档题．
练习册系列答案
相关题目
9．cos（-40°）cos20°-sin（-40°）•sin（-20°）等于．
| A． | -$\frac{1}{2}$ | B． | -$\frac{\sqrt{3}}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
6．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}-4x+6，x≥0}\\{x+6，x＜0}\end{array}\right.$，则不等式f（x）≥f（1）的解集是（ ）
| A． | [-3，1]∪（3，+∞） | B． | （-3，1）∪（2，+∞） | C． | （-1，1）∪（3，+∞） | D． | （-∞，-3）∪（1，3） |