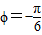题目内容
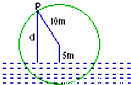 如图,一个半径为10米的水轮按逆时针方向每分钟转4圈,记水轮上的点P到水面的距离为d米(P在水面下则d为负数),则d(米)与时间t(秒)之间满足关系式:d=Asin(ωt+φ)+k(A>0,ω>0),
如图,一个半径为10米的水轮按逆时针方向每分钟转4圈,记水轮上的点P到水面的距离为d米(P在水面下则d为负数),则d(米)与时间t(秒)之间满足关系式:d=Asin(ωt+φ)+k(A>0,ω>0),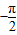 <φ<
<φ<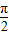 ,且当P点从水面上浮现时开始计算时间,有以下四个结论:
,且当P点从水面上浮现时开始计算时间,有以下四个结论:(1)A=10;
(2)ω=
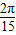 ;
;(3)φ=
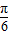 ;
;(4)K=5,
则其中所有正确结论的序号是 .
【答案】分析:先根据d的最大和最小值求得A和k;再根据每分钟转4圈算出周期,求得w;再根据当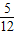 秒时d最大,求得φ.
秒时d最大,求得φ.
解答:解:由图可知d的最大值为15,最小值为-5即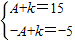 ,解得A=10,k=5,故(1)(4)正确.
,解得A=10,k=5,故(1)(4)正确.
∵每分钟转4圈,∴函数的周期为15s,故ω=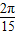 ,(2)正确.
,(2)正确.
依题意可知当5秒时,d最大进而求得φ=-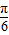 ,故(3)错误
,故(3)错误
故答案为:(1)、(2)、(4)
点评:本题主要考查了用y=Asin(ωx+φ)的部分图象确定解析式.属基础题.
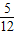 秒时d最大,求得φ.
秒时d最大,求得φ.解答:解:由图可知d的最大值为15,最小值为-5即
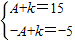 ,解得A=10,k=5,故(1)(4)正确.
,解得A=10,k=5,故(1)(4)正确.∵每分钟转4圈,∴函数的周期为15s,故ω=
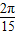 ,(2)正确.
,(2)正确.依题意可知当5秒时,d最大进而求得φ=-
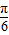 ,故(3)错误
,故(3)错误故答案为:(1)、(2)、(4)
点评:本题主要考查了用y=Asin(ωx+φ)的部分图象确定解析式.属基础题.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
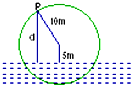 如图,一个半径为10米的水轮按逆时针方向每分钟转4圈,记水轮上的点P到水面的距离为d米(P在水面下则d为负数),则d(米)与时间t(秒)之间满足关系式:d=Asin(ωt+φ)+k(A>0,ω>0),
如图,一个半径为10米的水轮按逆时针方向每分钟转4圈,记水轮上的点P到水面的距离为d米(P在水面下则d为负数),则d(米)与时间t(秒)之间满足关系式:d=Asin(ωt+φ)+k(A>0,ω>0),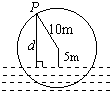 如图,一个半径为10米的水轮按逆时针方向每分钟转4圈.记水轮上的点P到水面的距离为d米(P在水面下则d为负数),则d(米)与时间t(秒)之间满足关系式:d=Asin(ωt+φ)+k(A>0,ω>0),
如图,一个半径为10米的水轮按逆时针方向每分钟转4圈.记水轮上的点P到水面的距离为d米(P在水面下则d为负数),则d(米)与时间t(秒)之间满足关系式:d=Asin(ωt+φ)+k(A>0,ω>0),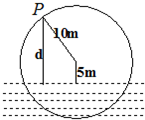 (2012•北京模拟)如图,一个半径为10米的水轮按逆时针方向每分钟转4圈.记水轮上的点P到水面的距离为d米(P在水面下则d为负数),如果d(米)与时间t(秒)之间满足关系式:
(2012•北京模拟)如图,一个半径为10米的水轮按逆时针方向每分钟转4圈.记水轮上的点P到水面的距离为d米(P在水面下则d为负数),如果d(米)与时间t(秒)之间满足关系式: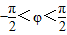 ,且当P点从水面上浮现时开始计算时间.则( )
,且当P点从水面上浮现时开始计算时间.则( )
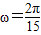 ,k=5
,k=5
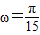 ,
,