题目内容
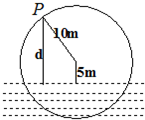 (2012•北京模拟)如图,一个半径为10米的水轮按逆时针方向每分钟转4圈.记水轮上的点P到水面的距离为d米(P在水面下则d为负数),如果d(米)与时间t(秒)之间满足关系式:d=Asin(ωt+φ)+k (A>0 , ω>0,-
(2012•北京模拟)如图,一个半径为10米的水轮按逆时针方向每分钟转4圈.记水轮上的点P到水面的距离为d米(P在水面下则d为负数),如果d(米)与时间t(秒)之间满足关系式:d=Asin(ωt+φ)+k (A>0 , ω>0,-| π |
| 2 |
| π |
| 2 |
分析:先根据d的最大和最小值求得A和k;再根据每分钟转4圈算出周期,求得ω;再根据当
秒时d最大,求得φ.
| 5 |
| 12 |
解答:解:由图可知d的最大值为15,最小值为-5即
,解得A=10,k=5,故A,D正确.
∵每分钟转4圈,∴函数的周期为15s,故ω=
,即B正确.
依题意,可知当t=0时,d=0,即10sinφ=-5,解可得φ=-
π,即C错误
故选C.
|
∵每分钟转4圈,∴函数的周期为15s,故ω=
| 2π |
| 15 |
依题意,可知当t=0时,d=0,即10sinφ=-5,解可得φ=-
| π |
| 6 |
故选C.
点评:本题考查三角函数的应用,考查用三角函数解决一些简单实际问题,考查函数y=Asin(ωx+φ)+k的实际意义,属于基础题.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 (2012•北京模拟)如图,在四棱锥P-ABCD中,PA⊥平面AC,且四边形ABCD是矩形,则该四棱锥的四个侧面中是直角三角形的有( )
(2012•北京模拟)如图,在四棱锥P-ABCD中,PA⊥平面AC,且四边形ABCD是矩形,则该四棱锥的四个侧面中是直角三角形的有( ) (2012•北京模拟)甲、乙、丙、丁四个人进行传球练习,每次球从一个人的手中传入其余三个人中的任意一个人的手中.如果由甲开始作第1次传球,经过n次传球后,球仍在甲手中的所有不同的传球种数共有an种.
(2012•北京模拟)甲、乙、丙、丁四个人进行传球练习,每次球从一个人的手中传入其余三个人中的任意一个人的手中.如果由甲开始作第1次传球,经过n次传球后,球仍在甲手中的所有不同的传球种数共有an种.