题目内容
【题目】如图,⊙O是等腰三角形ABC的外接圆,AB=AC,延长BC到点D,使CD=AC,连接AD交⊙O于点E,连接BE与AC交于点F. 
(1)判断BE是否平分∠ABC,并说明理由;
(2)若AE=6,BE=8,求EF的长.
【答案】
(1)解:BE平分∠ABC,理由如下:
证明:∵AC=CD,
∴∠CAD=∠ADC,
∴∠ACB=∠CAD+∠ADC=2∠CAD
又∵AB=AC,
∴∠ABC=∠ACB=2∠CAD,
∵∠CAD=∠EBC,
∴∠ABC=2∠EBC,
∴BE平分∠ABC
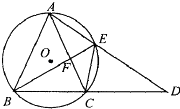
(2)解:连接EC,由(1)BE平分∠ABC,
∴E是弧AC的中点,
∴AE=EC=6,
又∠EBC=∠CAD=∠ADC,
∴ED=BD=8
∵A、B、C、E四点共圆,
∴∠CED=∠ABC=∠ACB=∠AEF
∴△AEF∽△DEC
∴ ![]() ,
,
∴EF= ![]() =
= ![]()
【解析】(1)BE平分∠ABC.由已知中边的相等,可得∠CAD=∠D,∠ABC=∠ACB,再利用同弧所对的圆周角相等,可得∠CAD=∠D=∠DBE,即有∠ABE+∠EBD=∠CAD+∠D,利用等量减等量差相等,可得∠EBD=∠D=∠ABE,故得证.(2)由(1)中的所证条件∠ABE=∠FAE,再加上两个三角形的公共角,可证△BEA∽△AEF,利用比例线段可求EF.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目