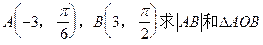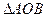题目内容
求圆心在A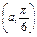 (a>0),半径为a的圆的极坐标方程.
(a>0),半径为a的圆的极坐标方程.
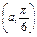 (a>0),半径为a的圆的极坐标方程.
(a>0),半径为a的圆的极坐标方程.所求的圆的极坐标方程为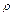 =2acos(
=2acos(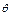 -
-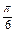 )
)
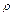 =2acos(
=2acos(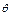 -
-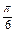 )
)如图所示,设M(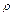 ,
,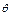 )为圆上的任意一点(点O,B除外),则OM=
)为圆上的任意一点(点O,B除外),则OM=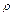 ,∠MOx=
,∠MOx=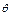 .
.
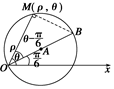
连结BM,OB=2a,∠MOB=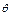 -
-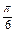 .
.
在直角三角形OBM中,
cos∠MOB=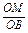 =
=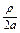
=cos(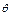 -
-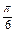 ),
),
即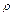 =2acos(
=2acos(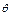 -
-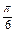 ).(*)
).(*)
经检验,O(0,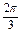 ),B(2a,
),B(2a,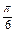 )满足方程(*),
)满足方程(*),
所以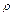 =2acos(
=2acos(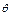 -
-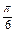 )为所求的圆的极坐标方程.
)为所求的圆的极坐标方程.
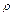 ,
,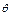 )为圆上的任意一点(点O,B除外),则OM=
)为圆上的任意一点(点O,B除外),则OM=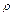 ,∠MOx=
,∠MOx=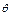 .
.
连结BM,OB=2a,∠MOB=
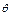 -
-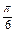 .
.在直角三角形OBM中,
cos∠MOB=
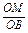 =
=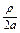
=cos(
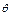 -
-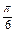 ),
),即
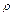 =2acos(
=2acos(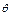 -
-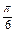 ).(*)
).(*)经检验,O(0,
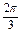 ),B(2a,
),B(2a,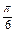 )满足方程(*),
)满足方程(*),所以
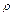 =2acos(
=2acos(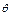 -
-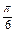 )为所求的圆的极坐标方程.
)为所求的圆的极坐标方程.
练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
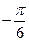 )到直线
)到直线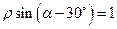 的距离是 。
的距离是 。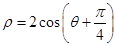 ,则该圆的半径是 .
,则该圆的半径是 .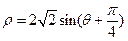 所表示的曲线的直角坐标方程是 。
所表示的曲线的直角坐标方程是 。
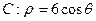 ,则圆C的半径为 。
,则圆C的半径为 。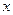 轴正半轴为极轴建立极坐标系,有下列命题:
轴正半轴为极轴建立极坐标系,有下列命题: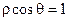 与曲线
与曲线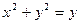 无公共点;
无公共点;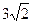 ,
,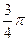 )的点
)的点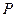 所对应的复数是-3+3i;
所对应的复数是-3+3i;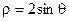 的圆心到直线
的圆心到直线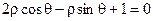 的距离是
的距离是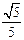 ;
; 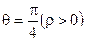 与曲线
与曲线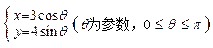 相交于点
相交于点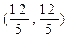 .
.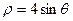 化为直角坐标方程为 .
化为直角坐标方程为 .