题目内容
已知极坐标系的极点与直角坐标系的原点重合,极轴与x轴的正半轴重合.若曲线C1的方程为ρ2=8ρsinθ-15,曲线C2的方程为
(α为参数).
(1)将C1的方程化为直角坐标方程;
(2)若C2上的点Q对应的参数为α=
,P为C1上的动点,求PQ的最小值.
|
(1)将C1的方程化为直角坐标方程;
(2)若C2上的点Q对应的参数为α=
| 3π |
| 4 |
(1)曲线C1的方程为ρ2=8ρsinθ-15化为直角坐标方程为:
x2+y2-8y+15=0;(3分)其圆心坐标(0,4),半径为:1.
(2)当α=
,时,得Q(-2,1)它到曲线C1的圆心C1(0,4)的距离为:
,
∴PQ的最小值
-1.
x2+y2-8y+15=0;(3分)其圆心坐标(0,4),半径为:1.
(2)当α=
| 3π |
| 4 |
| 13 |
∴PQ的最小值
| 13 |

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
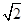 sin
sin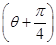 ,以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线
,以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线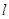 的参数方程为
的参数方程为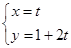 (t为参数),判断直线
(t为参数),判断直线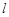 的参数方程为
的参数方程为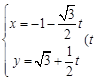 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,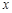 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆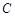 的极坐标方程为
的极坐标方程为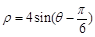 .求:
.求: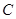 的直角坐标方程;
的直角坐标方程;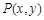 是直线
是直线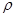 ≤
≤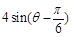 的公共点,求
的公共点,求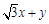 的取值范围.
的取值范围.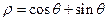 和直线
和直线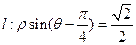 ,
, 的直角坐标方程;(2)当
的直角坐标方程;(2)当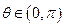 时,求直线
时,求直线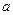
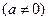 和
和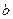 ,不等式
,不等式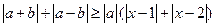 恒成立,试求实数
恒成立,试求实数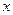 的取值范围.
的取值范围.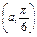 (a>0),半径为a的圆的极坐标方程.
(a>0),半径为a的圆的极坐标方程.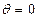 ,
,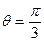 ,
,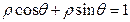 围成图形的面积是________
围成图形的面积是________ 
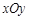 中,直线
中,直线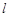 的参数方程是
的参数方程是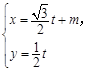 (t是参数), 以原点为极点,x轴的正半轴为极轴建立极坐标系,若圆C的极坐标方程是ρ=4cosθ,且直线
(t是参数), 以原点为极点,x轴的正半轴为极轴建立极坐标系,若圆C的极坐标方程是ρ=4cosθ,且直线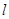 的参数方程为
的参数方程为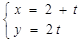 (t为参数),若以直角坐标系
(t为参数),若以直角坐标系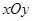 的
的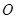 点为极点,
点为极点,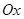 轴为极轴,选择相同的长度单位建立极坐标系,得曲线
轴为极轴,选择相同的长度单位建立极坐标系,得曲线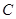 的极坐标方程为ρ=
的极坐标方程为ρ=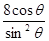 .
.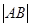 .
.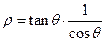 ,则曲线的直角坐标方程为________________。
,则曲线的直角坐标方程为________________。